The (Sir George) Stokes parameters provide a very useful description of the polarization state of an electromagnetic wave. Because of the importance of polarimetry in radio astronomy, I will give a brief description of Stokes parameters, their relation to the quantities measured by the ATCA and the ensuing ramifications for calibration purposes. See also the MIRIAD manual for good (we think) descriptions of polarimetric issues involving the ATCA and the ATNF scientific memorandum by Sault, Killeen, and Kesteven on ATCA polarization calibration.
The Stokes parameters are related to the amplitudes of the components of
the electric field, 
and 
, resolved in two perpendicular
directions normal to the direction of propogation. If 
and 
are represented by 
and 
, respectively, then the Stokes parameters are
defined as:
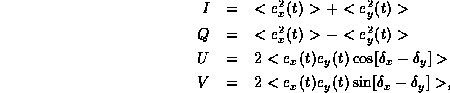
where the angle brackets denote a time average. The parameter I is a measure of the total power in the wave, Q and U represent the linearly polarized component, and V represents the circularly polarized component. These values can be converted to a measure of polarization as follows:
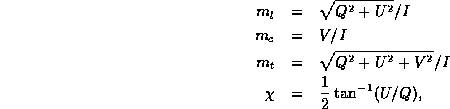
where 
, 
, and 
are the degrees of linear, circular and
total polarization, and 
is the position angle of the plane of
polarization. The Stokes parameters have the dimensions of flux density,
and they combine additively for independent waves.
The next question is how to relate the Stokes parameters to the correlations that an interferometer produces. In general, the response of an interferometer is a linear combination of two Stokes parameters, the combination determined by the polarization of each antenna (e.g. linear feeds for the ATCA or circular feeds for the VLA). By observing with different combinations of polarizations, all the Stokes parameters can be determined, and the complete state of the polarization of the wave found. For the interferometer, each Stokes parameter has a corresponding complex visibility. Therefore, the variation of each of the Stokes parameters over the source can be imaged individually, and the polarization of the radiation emitted from the source at any location determined. Note that in the image plane, I is always positive (ignoring noise, errors and beam sidelobes), whereas Q, U, and V may be positive or negative depending on the polarization position angle, or sense of rotation.
The correlations from an interferometer with perfectly linearly polarized feeds and identical gains are related to the Stokes parameters as follows:
where the X and Y feeds are orthogonal and in the equatorial reference frame of the source. It is instructive to look at the equations for telescopes (such as the VLA) with circularly polarized feeds as well. In this case,
In the discussion of § 3.1 there is no polarization
information explicitly included in the calibration equation; the model
must match the data. For circular feeds, the 
generally
represents the RR and LL visibilities and the calibrator model
source is assumed to be not circularly polarized so that RR and
LL respond purely to Stokes I. However, it is not so simple
for linear feeds. Here we associate the 
with the XX and
YY visibilities. But now, the model visibilities should really
include the fact that XX and YY respond to Stokes Q and
U as well as Stokes I. However, generally, we do not know
what the polarization characteristics of a calibrator are, so that this
is not straightforward. This is why it is more complex to calibrate
linearly polarized feeds compared to circularly polarized feeds.
The above equations are for ideal antennas. In reality, the feeds are not perfectly linearly polarized, so that an observation of an unpolarized sources yields a source which appears polarized. Furthermore, the feeds rotate with respect to the equatorial reference frame of the source, so that the above equations are not directly useable. A polarization calibration attempts to remove both these effects leaving just the source polarization in the data. For reference, the full set of equations is