Moment Analysis

The task moment can be used to generate moment images from a spectral-line cube. The moment axis should be either the first or third in the cube (e.g. vxy or xyv order). You should use reorder if you want the moment of the second axis for some reason. The moments (evaluated for each spatial pixel and along the velocity axis) are defined as

$$M_n = \int I(v) v^n dv$$

where I(v) is the intensity at a given velocity v. Thus, the zeroth moment corresponds to the integrated intensity over velocity, the first moment corresponds to the intensity weighted velocity, and the second moment corresponds to the intensity weighted velocity dispersion squared.

Note that moment is actually a little inconsistent in applying this equation depending on which moment it is working out. Here is what it finds:

$$M_0 = \int I(v) dv$$

in units of Jy km/s.

$$M_1 = {\int I(v) v dv \over {\int I(v) dv}}$$

in km/s.

$$M_2 = \sqrt{{\int I(v) (v-M_1)^2 dv \over {\int I(v) dv}}}$$

in km/s.

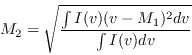
In the example we compute the second moment of a cube in xyv order excluding all pixels below 3-sigma which happens to be 2 mJy it seems; there is no point to adding noise to our sums. We select only the inner quarter of each spatial plane and we select only planes 40 to 480 for this analysis.

MOMENT
in=ngc253.icln	Input cube
region=quarter(40,480)	Select region
out=ngc253.m2	Output image
mom=2	Second moment
axis=3	Cube in xyv order
clip=0.002	Clip below this value