![]()
![]()
![]()
03(03.09.6; 03.09.2)
CSIRO, Australia Telescope National Facility, PO Box 76, Epping, 2121, Australia.
Calculating Quantization Correction Formulae for Digital Correlators with Digital Fringe Rotation.
P.P. Roberts.
17 March 1997
Abstract:
A method for calculating the conversion relationship between measured digital correlation and true analogue correlation, for digital correlators incorporating digital fringe rotation, is presented. Explicit expressions for the efficiency of correlators of this type are derived which can be used to optimise correlator system parameters. Results are presented for four correlation schemes in common use. Instrumentation: spectrographs - Instrumentation: Interferometers
Introduction
One of the principle differences between a VLBI correlator and a correlator as used on a connected-element array is that with the former fringe rotation is usually done digitally after the antenna signals have been sampled and recorded. This is because it is difficult to achieve a sufficiently low residual fringe rate for antennae spaced by many hundreds of kilometres by fringe rotating at the antennae. Since some precorrelation fringe rotation will usually be necessary to remove this residual fringe rate, it is simplest to do all the fringe rotation at this stage. This has the added advantage of allowing other sources within the primary beam of the array to be observed by simply changing the phase tracking centre to the new source.
A digital correlator operating on sampled signals estimates the correlation coefficient of the two original analog signals. It is essential to know the relationship between this digital estimate, based on sampled and quantized values of the input signals, and the true continuous correlation coefficient, so that the measured digital correlation can be corrected to what it would have been without quantization. As a result of the coarse one- or two-bit quantization used in radio astronomy this relationship is nonlinear. For a conventional correlator where fringe rotation is done by altering the phase of the local oscillator signal before sampling, a simple relationship can be derived based on the assumption that the signals entering the samplers have Gaussian statistics (Cooper 1970, Bowers and Klinger 1974). When one of the inputs is digitally fringe rotated before correlation this approach is no longer possible as the sequence of sample values coming from the digital fringe rotator forms a non-stationary time series, making conventional ergodic time series analysis invalid. In addition, the digital multiplier may have a biased characteristic. For example, in the case of a four-level correlator, as used on the Australia Telescope Long Baseline Array (AT LBA) correlator, it multiplies two four-level signals resulting in six possible output levels which must be reduced back to a four-level representation. Hence some multiplication products are biased relative to others, introducing further distortion.
The method generally used to quantify these effects is to introduce a loss factor, ![]() , the fringe rotation loss (Thompson et al. 1986). This describes the loss in signal-to-noise ratio, at small values of correlation, relative to a correlator without digital fringe rotation. To calculate the conversion relationship from measured digital correlation to the true correlation for the full range of correlation coefficient generally requires a lengthy computer simulation of the correlator although a constant scaling correction can be applied for small values of the correlation coefficient (Thompson et al. 1986). In the present work a method is presented which allows the conversion relationship to be calculated directly and permits an analytical expression for the signal-to-noise ratio performance of the correlator to be derived.
, the fringe rotation loss (Thompson et al. 1986). This describes the loss in signal-to-noise ratio, at small values of correlation, relative to a correlator without digital fringe rotation. To calculate the conversion relationship from measured digital correlation to the true correlation for the full range of correlation coefficient generally requires a lengthy computer simulation of the correlator although a constant scaling correction can be applied for small values of the correlation coefficient (Thompson et al. 1986). In the present work a method is presented which allows the conversion relationship to be calculated directly and permits an analytical expression for the signal-to-noise ratio performance of the correlator to be derived.
The VLBI correlator considered in this work is shown in Figure 1. This is a type of complex correlator. The sampled IF from one of the antennae is digitally multiplied by a digital approximation to a sine function to reduce the fringe rate to near zero. The input data streams are then correlated and the measured digital correlation at each lag corrected for distortion due to quantization. The correlation function is then Fourier transformed to give the cross power spectrum. Doing the same sequence of operations but with a digital sine function that is in quadrature to the original digital sine function results in a cross power spectrum with a ![]() phase difference compared to the first spectrum but with independent noise. Averaging the two spectra after correcting for the
phase difference compared to the first spectrum but with independent noise. Averaging the two spectra after correcting for the ![]() phase difference gives a spectrum with a signal to noise ratio
phase difference gives a spectrum with a signal to noise ratio ![]() greater than either of the individual spectra. The digital multiplier also produces an unwanted image response, but the fringes resulting from this image band generally have a high enough frequency that, with all but very low fringe rates, they are reduced to a negligible level by the time averaging of the correlator. In addition, the illustrated correlator configuration forms a single-sideband correlator. Any residual response to the image band differs in phase by
greater than either of the individual spectra. The digital multiplier also produces an unwanted image response, but the fringes resulting from this image band generally have a high enough frequency that, with all but very low fringe rates, they are reduced to a negligible level by the time averaging of the correlator. In addition, the illustrated correlator configuration forms a single-sideband correlator. Any residual response to the image band differs in phase by ![]() in the real and imaginary arms of the correlator so that, while the final
in the real and imaginary arms of the correlator so that, while the final ![]() phase shift and addition reinforces for the signal band, it cancels for the image band, removing the image response from the final spectrum.
phase shift and addition reinforces for the signal band, it cancels for the image band, removing the image response from the final spectrum.
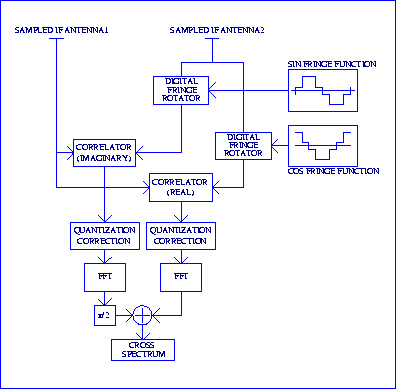
Figure1 The VLBI correlator architecture considered in this work.
Calculating the Conversion Function
Consider the signals received by two antennae observing the same source. There will, in general, be a different velocity component in the direction of the source at each antenna so that the correlated components in the two signals will be shifted in frequency, with the frequency difference being equal to the fringe rate. If the instantaneous correlation between the two signals were to be measured with a hypothetical perfect analog correlator it would be found to vary sinusoidally with time between ![]() and
and ![]() , where
, where ![]() is the correlation that would be measured for zero frequency offset (Fig. 2). This is an example of a cyclic cross correlation used to describe the general class of cyclo-stationary random processes (Gardner 1989).
is the correlation that would be measured for zero frequency offset (Fig. 2). This is an example of a cyclic cross correlation used to describe the general class of cyclo-stationary random processes (Gardner 1989).
Assuming that the joint distribution of the signal voltages S1 and S2 can be modelled by the bivariate normal distribution function, ![]() , where
, where ![]() is
is ![]() , for a particular value of correlation
, for a particular value of correlation ![]() , the probability that the quantized signals are in any particular state at a particular time can be calculated. For the AT LBA correlator four-level quantization is used, leading to 16 possible states for the combination of the two signals. Let this probability be denoted by
, the probability that the quantized signals are in any particular state at a particular time can be calculated. For the AT LBA correlator four-level quantization is used, leading to 16 possible states for the combination of the two signals. Let this probability be denoted by ![]() , which is the probability that S1 is in state i and S2 is in state j. Here, n is the correlator weighting given to samples in the outer level. The quantization scheme is illustrated in (1). The parameter v is the quantization threshold and the signals are assumed to be normalised to unit variance.
, which is the probability that S1 is in state i and S2 is in state j. Here, n is the correlator weighting given to samples in the outer level. The quantization scheme is illustrated in (1). The parameter v is the quantization threshold and the signals are assumed to be normalised to unit variance. 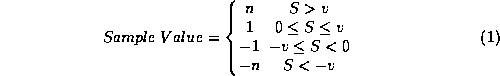
For zero mean signals of unit variance, with identical quantization threshold, v, the probabilities, ![]() , can be expressed in terms of the integral of the bivariate normal distribution function,
, can be expressed in terms of the integral of the bivariate normal distribution function, ![]() , as
, as 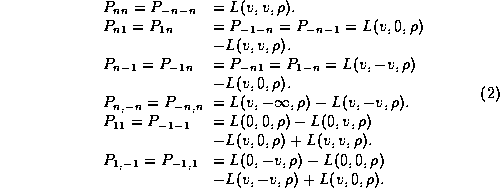
If one of the sample streams is now multiplied in a digital fringe rotator, the probability that the signals are in a certain state is altered depending on the characteristic of the multiplier and the phase of the fringe rotating function. The probability that the signals are in a particular state after fringe rotation, denoted by ![]() , and using the multiplier characteristic in Table 1, is given by
, and using the multiplier characteristic in Table 1, is given by 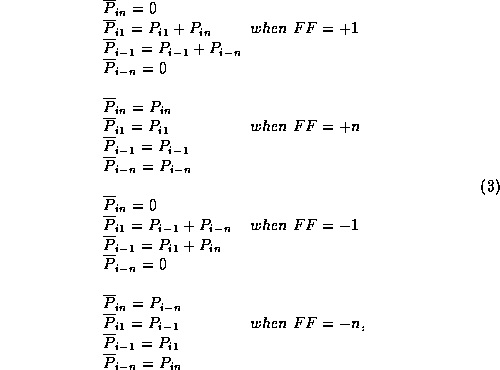
where FF is the state of the fringe rotation function.
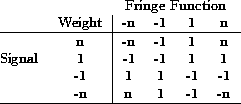
Table: Four-level multiplier characteristic
Consider the situation illustrated in Figure 2 where, for simplicity, the fringe rotation function is exactly in phase with the instantaneous correlation of the two signals. In general this would not be so but in practice the real and imaginary arms of the complex correlator would measure the in-phase and quadrature components of the correlation.

Figure 2 Instantaneous correlation and associated fringe rotation function.
At a particular phase ![]() the probability that the two signals are in state
the probability that the two signals are in state ![]() is given by
is given by ![]() , where
, where ![]() is the instantaneous correlation at that phase, and
is the instantaneous correlation at that phase, and ![]() the true correlation. Now consider the sequence of sample values at
the true correlation. Now consider the sequence of sample values at ![]() ,
, ![]() ,
, ![]() , ... ,
, ... , ![]() . The instantaneous correlation and state of the fringe rotator are the same for each sample in this sequence and so, since the original signals are assumed to be jointly stationary processes, and Nyquist sampling is assumed, the sequence forms a stationary time series. Hence the expected value of the product of the samples in this sequence can be calculated as
. The instantaneous correlation and state of the fringe rotator are the same for each sample in this sequence and so, since the original signals are assumed to be jointly stationary processes, and Nyquist sampling is assumed, the sequence forms a stationary time series. Hence the expected value of the product of the samples in this sequence can be calculated as
![]()
Repeating this for all the sample periods within ![]() of phase and averaging the result yields the mean correlator output. As the number of samples becomes large, this averaged sum approaches an integral and the final result for the mean correlator output is
of phase and averaging the result yields the mean correlator output. As the number of samples becomes large, this averaged sum approaches an integral and the final result for the mean correlator output is
![]()
or, by symmetry, ![]()
For this result to be correct it is strictly necessary that many fringe periods are contained within an integration and that there be an integral number of fringe periods within the integration. The first condition is satisfied except when the fringe rate is very low; the second condition is also only a problem when the fringe rate is low since, as the number of fringe periods in an integration becomes large, the error introduced by the non-integral number of periods becomes negligible. Dividing ![]() by R(1) yields the digital correlation coefficient.
by R(1) yields the digital correlation coefficient.
Signal-to-Noise Performance
Also of interest is the signal-to-noise ratio of the correlator measurement relative to an ideal correlator processing the same number of samples. This is known as the correlator efficiency. Most important is the efficiency when the correlation is small as this is the region in which the correlator generally operates. For two input sample streams, ![]() and
and ![]() , the correlator output is given by
, the correlator output is given by
![]()
where N is the number of samples processed. The variance of the correlator measurement is
![]()
where ![]() is the expectation.
is the expectation.
In the limit as the correlation approaches zero the second term approaches zero and the two processes become independent. Under these conditions, and with Nyquist sampling so that successive samples are uncorrelated, the expression for the variance reduces to
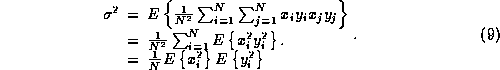
Hence the signal-to-noise ratio of the correlator measurement is
![]()
For the ideal case with no quantization this becomes
![]()
Thus the efficiency of the correlator is
![]()
This result applies to both the real and imaginary outputs of the complex correlator and so the final correlator efficiency is ![]() greater than (12).
greater than (12).
Two-level Correlator
As a simple example, consider the case of a pure one-bit correlator. Here the signal is quantized to ![]() according to whether the signal is greater or less than zero. In this case the fringe rotation function is a simple square wave of unit amplitude, and
according to whether the signal is greater or less than zero. In this case the fringe rotation function is a simple square wave of unit amplitude, and ![]() reduces to
reduces to ![]() . Hence the expected correlator output is
. Hence the expected correlator output is
![]()
Expanding the integrand by Taylor series and integrating term by term gives
![]()
The digital correlation coefficient is obtained by dividing this by the normalizing value R(1) = 0.5. This expression allows the digital correlation coefficient to be calculated to any desired accuracy although only a few terms are required for small correlations. To convert from measured digital correlation back to true correlation, the above series can be inverted or, as is more usual, a lookup table or interpolating function can be used.
In the pure one-bit case ![]() , and the correlator efficiency
, and the correlator efficiency ![]() 0.40. The complex correlator architecture increases this by
0.40. The complex correlator architecture increases this by ![]() to give 0.57. This compares with 0.64 for a one-bit correlator without digital fringe rotation (Cooper 1970).
to give 0.57. This compares with 0.64 for a one-bit correlator without digital fringe rotation (Cooper 1970).
Two-level Correlator with Three-level Fringe Rotation
In practice, most two-level correlators use a three-level fringe rotation function, where the fringe rotation function is zero for a portion of the cycle to give a better approximation to a sine function. The fringe rotation function so obtained is as shown in Figure 2, but with n equal to unity and the intermediate levels equal to zero. The three-level fringe rotation is implemented by blanking the correlator when the fringe rotation function is zero.
Using (6) the expected correlator output is 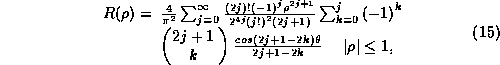
where ![]() is the phase at which the fringe rotation function jumps from zero to the higher level. The digital correlation coefficient is obtained by dividing by the normalizing value
is the phase at which the fringe rotation function jumps from zero to the higher level. The digital correlation coefficient is obtained by dividing by the normalizing value ![]() A graph of this conversion function is shown in Figure 3. Using (12) the correlator efficiency is given by
A graph of this conversion function is shown in Figure 3. Using (12) the correlator efficiency is given by ![]()
This has a maximum for (![]() ) where the efficiency has a value of 0.427, which is increased by the complex correlator architecture to 0.60. In practice, (
) where the efficiency has a value of 0.427, which is increased by the complex correlator architecture to 0.60. In practice, (![]() ) is used as this is an exact multiple of 1 / 16 of the full fringe period phase of
) is used as this is an exact multiple of 1 / 16 of the full fringe period phase of ![]() . This allows the fringe rotator phase to be represented as a four-bit digital quantity. There is virtually no loss in efficiency by using (
. This allows the fringe rotator phase to be represented as a four-bit digital quantity. There is virtually no loss in efficiency by using (![]() ) instead of (
) instead of (![]() ).
).
Four-Level Correlator
For the case of a two-bit, four-level correlator the expected correlator output cannot be solved for explicitly. Instead the integral (6) is solved numerically. Using the multiplier table give in Table 1, and an outer sample weighting of four, the conversion function shown in Figure 3 is found.
By using a first-order in ![]() approximation to the integral of the bivariate normal distribution function,
approximation to the integral of the bivariate normal distribution function,
![]()
and evaluating (6) and (12), an exact expression for the correlator efficiency can be derived. The efficiency in this case is a function of three variables: v - the threshold for samples to be considered in the outer level; n - the relative weighting for samples in the outer levels and ![]() - the phase at which the fringe rotation function jumps from the lower to the higher level. The result is
- the phase at which the fringe rotation function jumps from the lower to the higher level. The result is 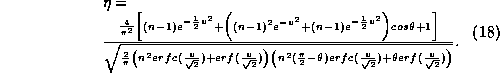
This function has a maximum at (v = 0.922, n = 3.84, ![]() = 0.544) where the efficiency is 0.602. Again, the complex correlator architecture increases this to 0.851. This compares to 0.88 for a four-level correlator without digital fringe rotation (Cooper 1970). In the AT LBA correlator (v = 0.94, n = 4.0,
= 0.544) where the efficiency is 0.602. Again, the complex correlator architecture increases this to 0.851. This compares to 0.88 for a four-level correlator without digital fringe rotation (Cooper 1970). In the AT LBA correlator (v = 0.94, n = 4.0, ![]() ) is used for simplicity in digital implementation and compatability reasons. There is only a slight drop in efficiency to 0.846.
) is used for simplicity in digital implementation and compatability reasons. There is only a slight drop in efficiency to 0.846.
Three-level Correlator
The three-level correlator, in which both the data and the fringe rotation function are quantized to three levels, is another scheme in use. The three-level correlator can be considered as a special case of the four-level correlator where both the inner levels are reassigned a weight of zero. As with the four-level correlator, the conversion function cannot be solved for explicitly. The numerically calculated conversion function is shown in Figure 3.
The efficiency of the three-level correlator can be derived from the expression for the four-level correlator efficiency by retaining only the terms in ![]() . The result is
. The result is
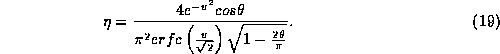
The efficiency is maximised for (![]() ) where it has a value of 0.389, increasing to 0.778 by virtue of the complex correlator architecture. This compares to 0.81 for a three-level correlator without digital fringe rotation. In practice (
) where it has a value of 0.389, increasing to 0.778 by virtue of the complex correlator architecture. This compares to 0.81 for a three-level correlator without digital fringe rotation. In practice (![]() ) is used with virtually no loss in efficiency.
) is used with virtually no loss in efficiency.
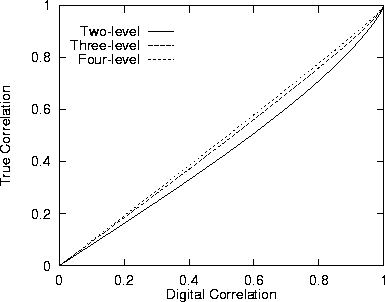
Figure 3 Conversion relationship for two- (![]() ), three-
), three-
(![]() ) and four-level (
) and four-level (![]() ) correlators with digital fringe rotation.
) correlators with digital fringe rotation.
Conclusion
A method has been demonstrated for calculating the conversion relationship between measured digital correlation and true analog correlation, for correlators incorporating digital fringe rotation. In addition, the method allows analytic expressions for the correlator efficiency to be derived. This is helpful for optimising correlator system parameters. Results for four correlator schemes have been derived but extension to other schemes is straightforward.
![]()
- 1970
- Cooper, B.F.C., 1970, Aust.J.Phys., 23, 521.
- 1974
- Bowers, F.K. and Klinger, R.J., A & AS, 1974, 15, 373.
- 1986
- Thompson, A.R., Moran J.M. and Swenson, G.W., 1986, In: Interferometry and Synthesis in Radio Astronomy. John Wiley, New York.
- 1989
- Gardner, W.A., 1989, In: Introduction to Random Processes. McGraw-Hill, New York.
About this document ...
Calculating Quantization Correction Formulae for Digital Correlators with Digital Fringe Rotation.
This document was generated using the LaTeX2HTML translator Version 96.1-h (September 30, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 fringe.tex.
The translation was initiated by Paul Roberts on Mon Apr 14 14:38:07 EST 1997
Paul Roberts
Mon Apr 14 14:38:07 EST 1997
