Radiale Masseverteilungen von Gaswolken
Konstante Massendichte
Der einfachste Fall einer radialsymmetrischen Masseverteilung in einer Gaswolke ist der einer konstanten Massendichte über das gesamte Volumen der Wolke. Diese Annahme ist zwar nicht besonders realistisch, aber sie läßt sich für einfache Abschätzungen physikalischer Parameter von Gaswolken sinnvoll verwenden. Wir setzen also für die Teilchendichte an:
\begin{equation*} n(r) = n_{0} \qquad (r \le h) . \end{equation*}
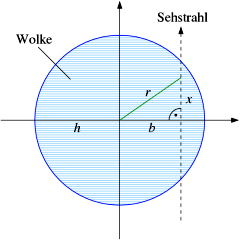
Hierbei bezeichne $h$ den Radius der Wolke. Dann ergibt sich die Säulendichte entlang der Sichtlinie in Richtung des Wolkenzentrums zu
\begin{equation*} N_{0} = 2 \int \limits_{0}^{\infty} \! n(r) \, \mathrm{d}r = 2 n_{0} h . \end{equation*}
Entsprechend erhalten wir für das Säulendichteprofil am Himmel senkrecht zur Sichtlinie die einfache Gleichung
\begin{equation*} N_{b} = 2 \int \limits_{0}^{\infty} \! n(x) \, \mathrm{d}x = 2 n_{0} \sqrt{h^{2} - b^{2}} \end{equation*}
für $b \le h$ (vgl. Abbildung rechts). Hierbei ist $b$ der Impaktparameter, das heißt der minimale Abstand des Sehstrahls vom Wolkenzentrum. Das Säulendichteprofil einer solchen Wolke am Himmel ist also von der Gestalt einer Kreisgleichung mit einem sehr flachen Verlauf in der Nähe des Zentrums und einem steilen Abfall gegen den Rand der Wolke hin. Ein solcher Verlauf der Säulendichte deckt sich nicht gut mit den beobachteten Profilen von Gaswolken, die eher eine gaußförmige Struktur aufweisen mit einem schmalen, spitzen Maximum und einem exponentiellen Abfall an den Flanken. Dennoch ist die Annahme einer konstanten Massendichte hin und wieder sinnvoll, weil sich damit physikalische Eigenschaften von Gaswolken schnell und einfach abschätzen lassen.
Quadratischer Abfall der Massendichte
Der einfachste Fall einer radial nach außen abfallenden Massendichte ist der eines quadratischen Abfalls mit dem Radius. Wir können den Dichteverlauf wie folgt ansetzen:
\begin{equation*} n(r) = \frac{n_{0} h^{2}}{h^{2} + r^{2}} \end{equation*}
worin $n_{0}$ wiederum die Dichte im Zentrum der Wolke bezeichnet und $h$ als eine Art Skalenlänge aufgefaßt werden kann. Ein linearer Abfall der Massendichte mit dem Radius ist nicht möglich, weil in diesem Fall die Dichte nicht schnell genug nach außen abfallen und daher die Säulendichte als Integral entlang des Sehstrahls durch die Wolke ins Unendliche anwachsen würde. Für den quadratischen Abfall der Dichte läßt sich wiederum leicht die beobachtete Säulendichte in Richtung des Wolkenzentrums berechnen:
\begin{equation*} N_{0} = 2 \int \limits_{0}^{\infty} \! n(r) \, \mathrm{d}r = 2 n_{0} \! \int \limits_{0}^{\infty} \! \frac{h^{2}}{h^{2} + r^{2}} \mathrm{d}r = \pi n_{0} h \end{equation*}
Für das Säulendichteprofil am Himmel erhalten wir in diesem Fall
\begin{equation*} N_{b} = 2 \int \limits_{0}^{\infty} \! n(x) \, \mathrm{d}x = 2 n_{0} \! \int \limits_{0}^{\infty} \! \frac{h^{2}}{h^{2} + b^{2} + x^{2}} \mathrm{d}x = \frac{\pi n_{0} h}{\sqrt{1 + b^{2} / h^{2}}} \end{equation*}
Dieser Säulendichteverlauf ist realistischer als im Fall der konstanten Massendichte. Das Säulendichteprofil weist im Zentrum das geforderte schmale, spitze Maximum auf. Jedoch ist der Abfall an den Flanken nicht steil genug, sondern geht für große $b$ mit $1/b$, so daß das Säulendichteprofil auffallend breite Flügel aufweist, die nicht mit der beobachteten Situation in Einklang stehen.
Exponentieller Abfall der Massendichte
Eine realistische Annahme über den Verlauf der Massendichte mit dem Radius ist die eines exponentiellen Abfalls. Wir können in diesem Fall die Teilchendichte zu
\begin{equation*} n(r) = n_{0} \exp({-r} / h) \end{equation*}
ansetzen. Hierbei ist $h$ die exponentielle Skalenlänge. Für die Säulendichte in Richtung des Zentrums der Wolke ergibt sich hierbei der sehr einfache Ausdruck
\begin{equation*} N_{0} = 2 \int \limits_{0}^{\infty} \! n(r) \, \mathrm{d}r = 2 n_{0} h \end{equation*}
den wir auch schon für den Fall der konstanten Massendichte erhalten hatten. Sehr kompliziert wird hingegen der radiale Verlauf der Säulendichte am Himmel. Wir erhalten
\begin{equation*} N_{b} = 2 \int \limits_{0}^{\infty} \! n(x) \, \mathrm{d}x = 2 n_{0} \! \int \limits_{0}^{\infty} \! \exp \left( \frac{\sqrt{x^{2} + b^{2}}}{-h} \right) \mathrm{d}x = 2 n_{0} b \, K_{1} \! \left( \frac{b}{h} \right) \end{equation*}
Hierin ist $K_{1}(x)$ die sogenannte modifizierte Besselfunktion erster Art und erster Ordnung. Sie ist definiert über
\begin{equation*} K_{1}(x) = {-\mathrm{i}} \, J_{1}(\mathrm{i} x) = \frac{x}{2} \sum \limits_{k \, = \, 0}^{\infty} \frac{(x^{2} / 4)^{k}}{k! \, \Gamma(k + 1)} \end{equation*}
worin $J_{1}(x)$ die gewöhnliche Besselfunktion erster Art und erster Ordnung ist und $\Gamma(x)$ die sogenannte Gamma-Funktion. $K_{1}(x)$ läßt sich auch in Integralform schreiben als
\begin{equation*} K_{1}(x) = \frac{1}{\pi} \! \int \limits_{0}^{\pi} \exp[x \cos(\vartheta)] \cos(\vartheta) \, \mathrm{d}\vartheta \end{equation*}
Für große $b$ nimmt das Säulendichteprofil nun einen exponentiellen Verlauf an, wie wir ihn bei realen Wolken auch beobachten.