Spherical geometry
Solid angle
The angle of a full circle is defined via the circumference of a circle with radius $r = 1$:
\begin{equation*} \frac{\vartheta}{\mathrm{rad}} = 2 \pi r = 2 \pi \end{equation*}
Hence, $360^{\circ} = 2 \pi~\mathrm{rad}$; accordingly, $1~\mathrm{rad} = (180^{\circ} / \pi) \approx 57.3^{\circ}$. In a very similar fashion one can define the solid angle of a full sphere as the surface area of a sphere with a radius of $r = 1$:
\begin{equation} \frac{\Omega}{\mathrm{sr}} = 4 \pi r^{2} = 4 \pi \label{eqn_solidangle} \end{equation}
Hence, the solid angle of the full sphere, e.g. the entire sky, is given by $4 \pi~\mathrm{sr}$. To convert this into square degrees, we can use the above definition and simply scale the radius such that the circumference of a circle with that radius is 360:
\begin{equation*} 2 \pi r = 360 \qquad \Rightarrow \qquad r \approx 57.3 \end{equation*}
Inserting this into Equation \eqref{eqn_solidangle} yields
\begin{equation*} \frac{\Omega}{\mathrm{deg}^{2}} = 4 \pi r^{2} \approx 41\,253 \end{equation*}
Hence, the full sky has a solid angle of about 40 000 square degrees, and the conversion factor between steradiant and square degree is thus given by
\begin{equation*} 1~\mathrm{sr} = \left( \frac{180^{\circ}}{\pi} \right)^{2} \approx \, 3\,283~\mathrm{deg}^{2} \end{equation*}
Spherical cap
The solid angle of a spherical cap, i.e. the surface of a cone of opening angle $2 \vartheta$, is given by
\begin{equation*} \frac{\Omega}{\mathrm{sr}} = 2 \pi \, [1 - \cos(\vartheta)] \end{equation*}
Note that $\vartheta$ is defined as half the opening angle of the cone.
Rectangular pyramid
The solid angle of a four-sided, rectangular pyramid with opening angles $\alpha$ and $\beta$ is given by
\begin{equation*} \frac{\Omega}{\mathrm{sr}} = 4 \arcsin \left[ \sin \left( \frac{\alpha}{2} \right) \sin \left( \frac{\beta}{2} \right) \right] . \end{equation*}
Note that all four sides of the pyramid form arcs of great circles.
Rectangle of longitude and latitude
In the case of a rectangle the boundaries of which are defined by lines of constant longitude, $l$, and latitude, $b$, the solid angle is given by
\begin{equation*} \frac{\Omega}{\mathrm{sr}} = [ \sin (b_{\rm N}) - \sin (b_{\rm S}) ] \times (l_{\rm E} - l_{\rm W}) \end{equation*}
where N, S, E and W denote the northern, southern, eastern and western boundary of the area, respectively. Note that only the eastern and western longitude boundaries lie on great circles, but not the latitude boundaries.
Solid angle of a telescope beam
Under the assumption that the beam of a telescope can be approximated by a two-dimensional, elliptical Gaussian function, we can calculate the solid angle of the beam by integrating over that Gaussian:
\begin{equation*} \Omega = \iint \! G(\alpha, \beta) \, \mathrm{d}\alpha \, \mathrm{d}\beta = \frac{\pi \vartheta_{a} \vartheta_{b}}{4 \ln(2)} \approx 1.133 \, \vartheta_{a} \vartheta_{b} \end{equation*}
Here, $\vartheta_{a}$ and $\vartheta_{b}$ are the FWHM of the beam’s major and minor axis, respectively. For example, at a frequency of $f = 1.4~\mathrm{GHz}$ the ATCA has a primary beam FWHM of $\vartheta_{a} = \vartheta_{b} = 36' = 0.6^{\circ}$, yielding a beam solid angle of $\Omega = 0.4~\mathrm{deg}^{2}$.
The angular separation of two points on a shpere
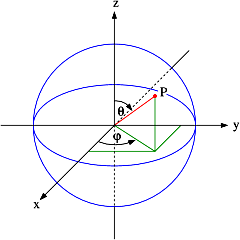One of the frequently needed parameters in astronomy is the angular distance between two objects in the sky. Let's assume a polar coordinate system with an azimuthal angle of $0 \le \varphi < 2 \pi$, a polar angle of $0 \le \vartheta \le \pi$ and a radius of unity $(r = 1)$. The figure on the right illustrates how the angles $\varphi$ and $\vartheta$ are defined. If we have two points, $\vec{p}_{1}$ and $\vec{p}_{2}$, on the sphere defined by the above coordinate system, we can easily determine their angular separation, $\alpha$, via
\begin{equation*} \vec{p}_{1} \cdot \vec{p}_{2} = p_{1} p_{2} \cos(\alpha) = \cos(\alpha) \end{equation*}
with $p_{1} \equiv |\vec{p}_{1}| = 1$ and $p_{2} \equiv |\vec{p}_{2}| = 1$. Substituting the angles $\varphi_{1}$, $\varphi_{2}$, $\vartheta_{1}$ and $\vartheta_{2}$ into the above equation yields
\begin{equation*} \cos(\alpha) = \cos(\vartheta_{1}) \cos(\vartheta_{2}) + \sin(\vartheta_{1}) \sin(\vartheta_{2}) \cos(\varphi_{1} - \varphi_{2}) . \end{equation*}
When using the above formula to determine the angular distance of two positions in the sky one has to keep in mind that the polar angle in celestial coordinate systems (e.g. the declination, $\delta$, or the Galactic latitude, $b$), is usually running from ${+\pi} / 2$ to ${-\pi} / 2$ rather than $0$ to $\pi$ so that a conversion into polar coordinates is necessary before calculating $\alpha$.
Alternatively, the equation can be slightly rewritten by swapping the sine and cosine terms of the polar angle,
\begin{equation*} \cos(\alpha) = \sin(\vartheta_{1}) \sin(\vartheta_{2}) + \cos(\vartheta_{1}) \cos(\vartheta_{2}) \cos(\varphi_{1} - \varphi_{2}) , \end{equation*}
to allow the polar angle, $\vartheta$, to run from ${+\pi} / 2$ to ${-\pi} / 2$, as is usually the case in astronomical and terrestrial coordinate systems.