Post-processing of detections¶

Once the list of detected objects has been obtained, there are several post-processing steps that can be utilised. We describe here mask optimisation, two-dimensional component fitting, and spectral index & curvature measurement.

Mask optimisation¶

The WALLABY team have provided an algorithm to optimise the source mask (equivalent to the Duchamp concept of growing detections), such that the integrated flux of the detection is maximised subject to the noise present. This has been provided to avoid issues with the fact that the Duchamp-based parameterisation makes use only of the detected pixels, so structure below the detection threshold is not taken into account. Growing the object in this way increases the number of faint pixels contributing to source parameterisation.

Unlike the Duchamp-derived “growing” algorithm (Selavy.flagGrowth=true), the growing process does not use a flux or signal-to-noise threshold. Rather, it adds elliptical annuli to the source until the total flux of the annulus is negative or a specified maximum number of iterations is reached. It does this for all channels within ±W50 of the central spectral channel.

Algorithm details¶

The algorithm is implemented in the following way:

Source detection is performed using the usual Duchamp/Selavy approaches. Note that the growing option can be used prior to the mask optimisation.
First step for a given object is to define the spectral range over which the optimisation is done. This is taken to be W50 either side of the centre of the detection (in turn, defined by the Duchamp parameter pixelCentre). All channels within this range are treated equally.
An ellipse is then fitted to the moment-0 map of the object. The moment-0 map uses the detected voxels only, so is dependent on the source-detection done prior to the mask optimisation.
If clobberPrevious=true, the source is pared back to the single pixel at the centre, which is used as the seed for the optimisation. Otherwise, we keep the existing mask and build on it.
The mask is then grown:

For each spatial pixel in the current mask, all neighbouring pixels not already in the mask that lie within the ellipse are included in a new object. This is done for every channel over the spectral range

If the flux of this object is positive, each of its pixels are added to the current mask,

The size of the ellipse is increased by 1 pixel in the major axis direction, and enough in the minor axis direction to preserve the shape.

This continues as long as the flux of the new “object” is positive, and the number of growing iterations is less than maxIter.
The parameterisation of the object is redone.
Once all objects have been done, the Duchamp merging process is re-run to cleanup any pairs of objects that may have intersected.

Note that the flux etc that is calculated for the object after the mask optimisation replaces the value that would have been calculated before it. At this point, if you want to know, say, the integrated flux of an object with and without this mask optimisation, you will need to run the algorithm twice. I am looking at providing this as an alternative flux measurement - at that point the code may be put into the Duchamp library proper, rather than just in Selavy.

The result of the mask optimisation does depend somewhat on what is done in the source-detection prior to its use. Using the growing method of Duchamp (flagGrowth=true and growthCut or growthThreshold) allows a good initial estimate of both the spectral range and the ellipse fitted to the moment-0 map. The optimised mask still tends to be larger than that from Duchamp-growing alone (at least from the limited testing done so far).

To aid evaluation of this algorithm, the mask FITS output of Duchamp has been enabled in Selavy, although only for the serial case. If running a multiple-node job, the mask will not be written. When written, the mask will be called selavy-MASK-IMG.fits, where the IMG refers to the input image.

Mask optimisation parameters¶

Parameter	Type	Default	Explanation
optimiseMask	bool	false	Whether to use the mask optimisation algorithm
optimiseMask.maxIter	int	10	The maximum number of iterations to do. The growing process stops if this is reached, or if the flux of the annulus is negative
optimiseMask.clobberPrevious	bool	true	If true, the algorithm starts with only the central pixel and grows out from there, after fitting an ellipse to the input detection. If false, the algorithm starts with the input mask already determined by the Duchamp algorithms.

Source fitting¶

For continuum images, we have implemented the ability to fit 2D Gaussian components to detected sources. Note that no such facility yet exists for 3D cubes. For the purposes of this section, we adopt the terminology used elsewhere of describing the detected objects (that is, collections of pixels above the detection threshold) as ‘islands’ which have ‘components’ fitted to them. For Selavy, the islands are the result of running the detection algorithms, and it is the islands that are written to the catalogue given by Selavy.outFile (defaulting to selavy-results.txt).

Setup¶

The fitting itself is done by the fitGaussian function from the casacore package. This returns a set of parameters for each Gaussian: peak flux, x-pixel centre, y-pixel centre, major axis FWHM, axial ratio, position angle.

The pixels that are used in the fit are chosen in one of two ways. If Selavy.Fitter.fitJustDetection=true, then only the island pixels (ie. those that were detected) are used in the fit - no “background” pixels are used. This avoid confusion with possible neighbouring sources.

Alternatively, if Selavy.Fitter.fitJustDetection=false, the fitting is done using all pixels in a box surrounding the island. This box is defined by padding a border of a minimum number of pixels (defined by the boxPadSize parameter) in all directions around the island pixels (moving out from the extremities of the detected pixels). Only the pixels lying within this box are used in the fit. This approach is more consistent with the approach used in the FIRST survey.

Note that all parameters governing the fitting require a Selavy.Fitter. prefix, but for convenience this is left out in the text that follows.

Noise determination¶

The noise level (ie. the standard deviation of the noise background) is used by the fitting function to weight the fitting function and obtain the chi-squared value. This noise level is not that used by the detection algorithm, but rather one obtained by finding the median absolute deviation from the median (MADFM) in a square box centred on the island’s peak pixel. The side length of the box is governed by the noiseBoxSize parameter, which defaults to 101 pixels. Note that it is different to the box mentioned above. The MADFM is converted to an equivalent rms for a Gaussian noise distribution (by dividing by 0.674888).

It is possible to do the fit without calculating the noise level, by seeting useNoise = false. This sets the pixel sigma value to 1 for each pixel, effectively removing the noise from the chi-squared calculation.

Initial estimation of parameters¶

The fitGaussian function requires an initial estimate of the parameters. There are two ways Selavy obtains this initial estimate. The first way (the default) uses the following recursive algorithm to provide a list of sub-components (being distinct peaks within an island):

Using the island pixels, define a set of parameters: peak flux and location are obvious, while the major & minor axes & position angle are obtained from Duchamp algorithms, using a separate detection process at half the peak flux (to get the full width at half maximum).
Define a set of sub-thresholds (the number of these is given by the numSubThresholds parameter) spaced either linearly or logarithmically between the peak flux and the detection threshold (the separation between sub-thresholds is constant in either log or linear space depending on whether the input parameter logarithmicThresholds is true or false).
For each threshold, search the box surrounding the object, and record the number of separate detections.

If there is more than one separate object, call the getSubComponentList function on each of these and add the result to the vector list.

When you reach the final threshold, add the initial set of parameters to the vector list and return the vector list.

The second approach attempts to replicate the algorithm described in Hancock et al. (2012), MNRAS 422, 1812 (which is used in Paul’s ‘Aegean’ source-finder). This creates a curvature map using a discrete 2D Laplacian kernel. The curvature map, in combination with the mask of detected pixels, is used to locate local maxima within the island. The image is convolved with the 3x3 kernel - note that this means the single row of pixels around the edge will not have a curvature value assigned.

A point source is placed at each local maxima to provide the initial estimate of components. To use this mode, set useCurvature=true. The curvature map can be saved to a CASA image by setting the curvatureImage parameter.

If the Gaussian fitting fails to provide a good fit, these initial estimates can be returned as the results, with a flag indicating they are only estimates. Whether this is done is governed by the parameter useGuessIfBad, which defaults to true. If an estimate is reported in the results output, the final column Guess? will take the value 1, else it will be 0.

Fitting¶

If numGaussFromGuess=true (the default), the number of Gaussians that are fitted to the island is exactly equal to the number of subcomponents in the initial estimate. If, however, numGaussFromGuess=false, then the number of Gaussians fitted is between 1 and maxNumGauss. The subcomponents are chosen as initial estimates in order of their peak flux. If there are more Gaussians needed than there are subcomponents, we simply cycle through the list.

The fitting is done by casacore’s fitGaussian function. The fit is repeated a further two times, each time using the output of the previous fit as the initial guess. This results in a slight refinement of the fit, usually (but not always!) improving the chi-squared value.

The parameters that are fitted to the data are defined by the fitType parameter. This can take one of the following values:

full: All six parameters of the Gaussian are free to be fitted to the data.
psf: Only the position and height of the Gaussian are fitted. The size & shape are fixed to match the beam size, taken from the image header (or the beamSize parameter if the image header does not have the beam information).
shape: Only the position and shape of the Gaussian are fitted. The height is fixed to match the peak pixel flux of the object.
height: Only the height of the Gaussian is fitted, with the location and shape kept constant.

All types can be given in vector format to the fitType parameter. In this case, all listed types of fits are done, and the best result (judged by the reduced chi-squared value) is chosen as the best fit. This means that if the best fit for the “full” case is a beam-sized Gaussian, the fit from the “psf” case will be chosen as it has more degrees of freedom and so a lower reduced chi-squared.

When numGaussFromGuess=true and the fit converges but is poor, we test to see if an additional, confused component is present (that was not picked up by the original initial estimate). The fitted Gaussian is subtracted from the pixels, then the initial estimation algorithm is re-run. The brightest component found is added to the initial estimates provided to the fitting routine, and the fit is re-run with one extra Gaussian. This process continues until the fit does not converge.

Accepting the fit¶

The default tests to accept a fit result are the following:

The fit must have converged.
The chi-squared value is examined in one of two ways. The second method is used provided the chisqConfidence parameter is between 0 and 1. Otherwise (the default case), the first method is used.

The reduced chi-squared is compared to the maxReducedChisq parameter, and accepted if smaller. (Here we define rchisq = chisq / (npix - numGauss*nfree - 1), where nfree is the number of free parameters : See below for discussion)

The chi-squared value and the number of degrees of freedom are used to calculate the probability of a chi-squared-distributed parameter having the given value or less, and compared to the chisqConfidence level. For numbers of degrees of freedom greater than 343, computational requirements mean this is approximated by requiring the reduced chi-squared to be less than 1.2.

The peak flux of each component must be positive, unless negativeFluxPossible=true is set.
The centre of each component must be inside the box
The signal-to-noise (ratio of value to error from the fit) for the flux, major axis, and minor axis must all be larger than one.

If applyAcceptanceCriteria=true, we then apply a further set of criteria, that follow those used in the FIRST survey (Becker, White & Helfand 1995). These are:

The separation between any pair of components must be more than 2 pixels
The flux of each component must be positive and more than half the detection threshold
No component’s peak flux can exceed twice the highest pixel in the box.
The sum of the integrated fluxes of all components must not be more than twice the total flux in the box.

The results of each of these tests is printed to the log as a 1 (pass) or a 0 (fail).

If numGaussFromGuess=true, then we only use the same number of Gaussians as the number of components in the initial estimate. If this is false, the the behaviour is governed by the stopAfterFirstGoodFit parameter. If stopAfterFirstGoodFit=true, once the first acceptable fit is found (starting with a single Gaussian), the fitting is stopped. Multiple Gaussians are fitted only if fewer Gaussians do not give an acceptable fit. If stopAfterFirstGoodFit=false then the fitting using one through to the maximum number of Gaussians, and the best fit is chosen to be the one that passes all the above criteria and has the lowest reduced chi-squared value.

Given the above, however, Selavy will react to fits that are unacceptable in the following way:

If the fit fails to converge, and there was more than one Gaussian being fitted, then Selavy will try again with one fewer Gaussian (unless it has already tried that number).
If the fit converges, but has a high chi-squared value, Selavy will remove the fitted components and search for any further components that may have been missed with the initial search. The brightest of any found is added to the list of initial estimates, and the fit is re-done. This process can recover additional components that do not stand out as separate peaks when all components are present.

A note on the reduced chi-squared¶

The expression used to calculate the reduced chi-squared as shown above is fine if the pixels are independent. However, this is not the case for radio data, where neighbouring pixels are correlated due to the finite beam size. It is not immediately obvious what the correct way to estimate the reduced chi-squared is. It may be that, formally, a different metric should be used in assessing the goodness-of-fit (since an underlying assumption of the chi-squared test is that the pixels are independent).

Note that, leaving aside the formal requirements of the statistical test, this is primarily a problem when comparing different successful fits that have different numbers of Gaussians. The determination of the best fit for a given number of Gaussians should not be affected (although the second of our acceptance criteria might have to change).

Output files¶

Component Catalogue¶

Several files are produced to show the results of the Gaussian fitting. The first is a CASDA-compliant components catalogue. In pipeline operation, this would be the catalogue sent to CASDA, the CSIRO ASKAP Science Data Archive. This takes its name from the Selavy.resultsFile parameter, replacing the .txt extension with .components.txt. An XML/VOTable version is also produced (always), with a .xml extension.

The precision of particular columns can be changed with the precXXXX parameters described at the end of Selavy Basics. They should be left as defaults for upload to CASDA, unless instructed otherwise.

An example of the text version of this catalogue is shown here:

#         island_id          component_id component_name ra_hms_cont dec_dms_cont ra_deg_cont dec_deg_cont     ra_err    dec_err   freq  flux_peak flux_peak_err flux_int flux_int_err maj_axis min_axis pos_ang maj_axis_err min_axis_err  pos_ang_err maj_axis_deconv min_axis_deconv pos_ang_deconv maj_axis_deconv_err min_axis_deconv_err pos_ang_deconv_err chi_squared_fit rms_fit_gauss spectral_index spectral_curvature spectral_index_err spectral_curvature_err  rms_image has_siblings fit_is_estimate spectral_index_from_TT flag_c4                                                                                             comment
#                --                    --                                               [deg]        [deg]   [arcsec]   [arcsec]  [MHz] [mJy/beam]    [mJy/beam]    [mJy]        [mJy] [arcsec] [arcsec]   [deg]     [arcsec]     [arcsec]        [deg]        [arcsec]        [arcsec]          [deg]            [arcsec]            [arcsec]              [deg]              --    [mJy/beam]             --                 --                 --                     -- [mJy/beam]
    SB2338_island_1   SB2338_component_1a J221655-452149  22:16:55.2    -45:21:49  334.230130   -45.363683       0.09       0.07 1400.5   1877.111        12.318 2165.969       20.689    33.45    23.95   74.68         0.22         0.08         0.79           15.08            4.60         -87.62                1.00               13.76               1.13         686.286      4782.906           0.00               0.00               0.00                   0.00      2.916            0               0                      1       1
    SB2338_island_2   SB2338_component_2a J221021-454251  22:10:21.5    -45:42:51  332.589424   -45.714267       0.32       0.36 1400.5    811.963        17.958 1391.736       39.933    43.87    27.13   36.09         0.98         0.23         1.80           33.63            9.24          26.57                0.13                2.90               1.88        4966.390     11142.699           0.00               0.00               0.00                   0.00      2.262            0               0                      1       1
    SB2338_island_3   SB2338_component_3a J221105-433313  22:11:05.3    -43:33:13  332.772286   -43.553874       0.07       0.05 1400.5    884.571         4.219  928.795        6.669    32.49    22.44   70.75         0.16         0.06         0.51           12.04            0.00          81.97                0.80                0.00               0.74         209.765      2787.307          -0.00               0.00               0.00                   0.00      1.631            0               0                      1       0
    SB2338_island_4   SB2338_component_4a J222254-452730  22:22:54.3    -45:27:30  335.726258   -45.458383       0.14       0.11 1400.5    494.099         4.639  693.789        8.906    36.76    26.53   75.50         0.35         0.12         1.14           21.37           12.40          88.23                0.28                1.15               1.05         439.707      3766.180           0.00               0.00               0.00                   0.00      1.515            0               0                      1       1
    SB2338_island_5   SB2338_component_5a J221416-425710  22:14:16.8    -42:57:10  333.569959   -42.953043       0.05       0.04 1400.5    538.313         1.863  622.263        3.127    34.77    23.09   75.13         0.12         0.04         0.34           17.65            0.00          86.46                0.12                0.00               0.35         174.815      2374.698          -0.00               0.00               0.00                   0.00      0.900            0               0                      1       0
    SB2338_island_6   SB2338_component_6a J215840-471934  21:58:40.9    -47:19:34  329.670361   -47.326273       0.07       0.07 1400.5    374.492         2.079  471.220        3.714    32.58    26.81   49.71         0.18         0.08         1.15           16.56            7.90           5.86                0.22                1.33               0.56         202.162      2220.534           0.00               0.00               0.00                   0.00      1.027            1               0                      1       0
    SB2338_island_6   SB2338_component_6b J215834-471931  21:58:34.5    -47:19:31  329.643940   -47.325282       1.63       1.30 1400.5     19.343         2.557   21.011        4.164    31.75    23.75   88.85         4.14         1.94        18.90           15.15            0.00         -61.47                3.21                0.00               7.16         202.162      2220.534           0.00               0.00               0.00                   0.00      1.027            1               0                      1       0
    SB2338_island_7   SB2338_component_7a J221804-461322  22:18:04.8    -46:13:22  334.519855   -46.222850       0.23       0.15 1400.5    281.466         3.426  470.890        7.475    46.59    24.93   69.10         0.58         0.11         0.74           35.39            9.79          70.19                0.04                1.27               0.94         283.404      3073.564          -0.00              -0.00               0.00                   0.00      1.492            0               0                      1       0

The columns are:

Annotation files & maps of components¶

Along with the components catalogue, a matching Karma/CASA/DS9 annotation (region) file will be produced showing the location & size of the components (each Gaussian component is indicated by an ellipse given by the major & minor axes and position angle of the component). These are named in the same way as the catalogue file, but with a .ann/.crf/.reg extension respectively. Whether these are produced is governed by the flagKarma/flagCasa/flagDS9 parameters (see Selavy Basics for details).

By setting Fitter.writeComponentMap=true (the default), an image is made showing just the fitted Gaussian components. This is the “component map”. At the same time, a residual map (input image with the component map subtracted) is created. These default to being FITS files, unless Fitter.imagetype=casa is given. If imagename is the input image given to Selavy, the name of these images will be componentMap_*imagename*.fits and componentResidual_*imagename*.fits (with no “.fits” extension for casa images),

General fit results catalogue¶

A similar output file is the fit Results catalogue. This is only produced when writeFitResults=true. This shows the fit results with a different emphasis (this is the original method of showing the fit results in Selavy). This too takes its name from the Selavy.resultsFile parameter, replacing the .txt extension with .fitResults.txt. An example start for the file is as follows below.

#    ID           Name         RA        DEC       X       Y    F_int     F_peak F_int(fit)  F_pk(fit) Maj(fit) Min(fit) PA(fit) maj_axis_err min_axis_err  pos_ang_err Maj(fit_deconv) Min(fit_deconv) PA(fit_deconv) maj_axis_deconv_err min_axis_deconv_err pos_ang_deconv_err   Alpha    Beta spectral_index_err spectral_curvature_err Chisq(fit) RMS(image)   RMS(fit) Nfree(fit) NDoF(fit) NPix(fit) NPix(obj) fit_is_estimate
#    --             --      [deg]      [deg]   [pix]   [pix]    [mJy] [mJy/beam]      [mJy] [mJy/beam] [arcsec] [arcsec]   [deg]     [arcsec]     [arcsec]        [deg]        [arcsec]        [arcsec]          [deg]            [arcsec]            [arcsec]              [deg]      --      --                 --                     --         -- [mJy/beam] [mJy/beam]         --        --        --        --
     1a J221655-452149 334.230130 -45.363683 1454.46 1721.87  391.352   1726.833   2165.969   1877.111    33.45    23.95   74.68         0.22         0.08         0.79           15.08            4.60         -87.62                1.00               13.76               1.13    0.00    0.00               0.00                   0.00    686.286      2.916   4782.906          6        23        30        30               0
     2a J221021-454251 332.589424 -45.714267 1800.17 1619.95  246.408    766.953   1391.736    811.963    43.87    27.13   36.09         0.98         0.23         1.80           33.63            9.24          26.57                0.13                2.90               1.88    0.00    0.00               0.00                   0.00   4966.390      2.262  11142.699          6        33        40        40               0
     3a J221105-433313 332.772286 -43.553874 1760.88 2268.01  168.103    880.182    928.795    884.571    32.49    22.44   70.75         0.16         0.06         0.51           12.04            0.00          81.97                0.80                0.00               0.74   -0.00    0.00               0.00                   0.00    209.765      1.631   2787.307          6        20        27        27               0
     4a J222254-452730 335.726258 -45.458383 1140.46 1684.45  123.720    426.248    693.789    494.099    36.76    26.53   75.50         0.35         0.12         1.14           21.37           12.40          88.23                0.28                1.15               1.05    0.00    0.00               0.00                   0.00    439.707      1.515   3766.180          6        24        31        31               0
     5a J221416-425710 333.569959 -42.953043 1585.47 2447.06  112.662    493.966    622.263    538.313    34.77    23.09   75.13         0.12         0.04         0.34           17.65            0.00          86.46                0.12                0.00               0.35   -0.00    0.00               0.00                   0.00    174.815      0.900   2374.698          6        24        31        31               0
     6a J215840-471934 329.670361 -47.326273 2393.13 1125.49   87.930    329.294    471.220    374.492    32.58    26.81   49.71         0.18         0.08         1.15           16.56            7.90           5.86                0.22                1.33               0.56    0.00    0.00               0.00                   0.00    202.162      1.027   2220.534          6        28        41        41               0
     6b J215834-471931 329.643940 -47.325282 2398.50 1125.59   87.930    329.294     21.011     19.343    31.75    23.75   88.85         4.14         1.94        18.90           15.15            0.00         -61.47                3.21                0.00               7.16    0.00    0.00               0.00                   0.00    202.162      1.027   2220.534          6        28        41        41               0
     7a J221804-461322 334.519855 -46.222850 1399.46 1462.93   81.990    261.075    470.890    281.466    46.59    24.93   69.10         0.58         0.11         0.74           35.39            9.79          70.19                0.04                1.27               0.94   -0.00   -0.00               0.00                   0.00    283.404      1.492   3073.564          6        23        30        30               0

The columns provided are:

ID is a unique ID for the component. It comprises the ID number of the island, plus one or more characters indicating the order of components for that island. These will be a-z for the first 26, then aa-zz, then aaa-zzz and so forth.
Name is the name taken from the island.
RA, Dec, X and Y are the world and pixel locations of the component.
F_int and F_peak are values for the island as calculated by the Duchamp code, and reported in the Duchamp results file given by Selavy.outFile. These are the same for each comonent of that island.
F_int(fit) and F_pk(fit) are the integrated & peak fluxes from the fitted Gaussians.
Alpha and Beta are the spectral index and spectral curvature terms (with associated errors). These are only provided when the appropriate flags are set - see Spectral Terms.
Maj, Min and P.A. are the major and minor FWHMs and the position angle of the fitted Gaussian, quoted for both the fit and the fit deconvolved by the beam, with errors for each version.
The goodness of fit is indicated by the Chisq(fit) and RMS(fit) values, while RMS(image) gives the local noise surrounding the object.
Nfree(fit) is the number of free parameters in the fit, and NDoF(fit) is the number of degrees of freedom.
Npix(fit) is the number of pixels used in doing the fit, and Npix(obj) is the number of pixels in the object itself (ie. detected pixels).
A value of 1 in the fit_is_estimate column indicates that the “fitted” parameters come from the initial estimate (the fitting procedure failed for some reason).

If no fit was made (see components 1a and 1b in the example above), the Gaussian parameters are taken from the initial estimate, while those parameters relating to the quality of the fit are set to zero (for RMS, Nfree etc) or 999 (chisq).

A VOTable version of the fit results is also produced, with a .xml suffix. This is always produced whenever the fit results file is produced.

As well as the “best” fit catalogue, a catalogue of fit results is written for each fitType considered (out of ‘full’,’psf’,’shape’ and ‘height’). These will be named, for instance, selavy-results.fitResults.full.txt.

Two types of annotation files will also be produced:

Fitted components - a Karma/CASA/DS9 annotation (region) file showing the fitting results (each Gaussian component is indicated by an ellipse given by the major & minor axes and position angle of the component). These are named in the same way as the fit results file, but with a .ann/.crf/.reg extension respectively. Whether these are produced is governed by the flagKarma/flagCasa/flagDS9 parameters (see Selavy Basics for details).
fitBoxAnnotationFile [selavy-fitResults.boxes.ann] - an annotation file showing the boxes used for the Gaussian fitting (if boxes were not used, ie. fitJustDetection=true, this file is not created).

Component parset¶

The user can request that a component parset be created, showing the fitted components. Such a file could be used in tasks such as ccalibrator, for self-calibration, or csimulator. This file is created by providing a filename with the Selavy.outputComponentParset parameter. By default, all components are written, but you can specify a maximum number to be included using the Selavy.outputComponentParset.maxNumComponents parameter (the list is ordered by flux, so that the brightest ones are written first). The shape of the components is included by default, but you can force them to be point sources by setting Selavy.outputComponentParset.reportSize=false. See csimulator for details on how components should be specified.

Parameters for fitting¶

Parameter	Type	Default	Description
Basic control parameters
Selavy.distribFit	bool	true	If true, the edge sources are distributed by the master node to the workers for fitting. If false, the master node does all the fitting.
Selavy.Fitter.doFit	bool	false	Whether to fit Gaussian components to the detections
Selavy.Fitter.fitJustDetection	bool	true	Whether to use just the detected pixels in finding the fit. If false, a rectangular box is used.
Selavy.Fitter.fitTypes	vector<string>	[full,psf]	A vector of labels for the types of fit to be done. The input format needs to be a comma-separated list enclosed by square brackets (as in the default). The possible options are ‘full’, ‘psf’, ‘shape’, or ‘height’. See text above for details.
Selavy.Fitter.maxNumGauss	int	4	The maximum number of Gaussians to fit to a single detection. Ignored if numGaussFromGuess=true.
Selavy.Fitter.boxPadSize	int	3	When fitJustDetection=false, a border of at least this size is added around the detection to create a rectangular box in which the fitting is done.
Selavy.Fitter.stopAfterFirstGoodFit	bool	true	Whether to stop the fitting when an acceptable fit is found, without considering fits with more Gaussian components. Ignored if numGaussFromGuess=true.
Initial estimates
Selavy.Fitter.numGaussFromGuess	bool	true	Whether the number of Gaussians fitted should be the same as the number of components in the initial estimate (the “guess”). If false, the maximum number is taken from maxNumGauss.
Selavy.Fitter.numSubThresholds	int	20	The number of levels between the detection threshold and the peak that is used to search for subcomponents.
Selavy.Fitter.logarithmicThresholds	bool	true	Whether the sub-thresholds should be evenly spaced in log-space (true) or linear-space (false)
Selavy.Fitter.useCurvature	bool	false	Whether to find the initial component estimates from the curvature map instead of the sub-thresholding.
Selavy.Fitter.curvatureImage	string	<No default>	The name of the CASA image in which to write the curvature map. It will be made the same size as the input image.
Selavy.Fitter.useGuessIfBad	bool	false	Whether to print the initial estimates in the case that the fitting fails
Quality control parameters
Selavy.Fitter.maxReducedChisq	float	5.0	The maximum value for the reduced chi-squared for a fit to be acceptable.
Selavy.Fitter.chisqConfidence	float	-1.0	A probability value, between 0 and 1, used as a confidence level for accepting the chi-squared value. If outside this range of values (as is the default), the test is done with the reduced chi-squared value, using the maxReducedChisq parameter.
Selavy.Fitter.maxRMS	float	1.0	The value that is passed to the FitGaussian::fit() function.
Selavy.Fitter.useNoise	bool	true	Whether to measure the noise in a box surrounding the island and use that as the sigma value for each point in the fit. Setting to false has the effect of setting the sigma to one for each point.
Selavy.Fitter.noiseBoxSize	int	101	The side length of a box centred on the peak pixel that is used to estimate the noise level (ie. the rms) for a source: this is used for the fitting.
Selavy.Fitter.minFitSize	int	3	The minimum number of detected pixels that an island has for it to be fit.
Selavy.Fitter.maxIter	int	1024	The maximum number of iterations in the fit.
Selavy.Fitter.maxRetries	int	0	The maximum number of retries used by the fitting routine (ie. the maxRetries parameter for casa::FitGaussian::fit()).
Selavy.Fitter.criterium	double	0.0001	The convergence criterium for casa::FitGaussian::fit() (this does not seem to be used in the fitting).
Selavy.Fitter.negativeFluxPossible	bool	false	Whether we accept negative-flux components.
Selavy.Fitter.applyAcceptanceCriteria	bool	false	Whether to apply the full set of acceptance criteria above. If false, only the limited set will be applied.
Output files
Selavy.Fitter.writeComponentMap	bool	true	Whether to write out an image showing the fitted Gaussian components, as well as a “fit residual” map (the input image with the component map subtracted).
Selavy.Fitter.imagetype	string	fits	Type of image to write - either “casa” or “fits”.
Selavy.writeFitResults	bool	false	Whether to write out the fitResults files (catalogues and annotations).
Selavy.fitBoxAnnotationFile	string	selavy-fitResults.boxes.ann	A Karma annoation file showing the location and size of boxes used in the Gaussian fitting (only produced if Fitter.fitJustDetection = false).
Selavy.outputComponentParset	bool	false	Whether to write out a component parset.
Selavy.outputComponentParset.filename	string	<No default>	The name of the file to which the component parset should be written.
Selavy.outputComponentParset.maxNumComponents	int	-1	The maximum number of components to be written to the parset. If negative (the default), all will be written.
Selavy.outputComponentParset.referenceDirection	vector<string>	“”	The direction that is used as the reference (tangent point), from which the positions are calculated as l & m coordinates. If left blank, the image centre position will be used. This should be in the same format as given for the direction parameters in (cimager) (ie. a 3-element vector).
Selavy.outputComponentParset.reportSize	bool	true	If true, the fitted shape of the components is written to the parset. If false, they are written as point sources.

Spectral Index & Curvature¶

Measuring spectral terms from Taylor-term images¶

Selavy is designed to work in conjunction with the ASKAPsoft pipeline. For continuum data, a common processing mode will be multi-frequency synthesis, where the output will be a series of “Taylor-term” images, being the coefficients of a Taylor-expansion of the frequency spectrum at each pixel. The equations governing this expansion are indicated here

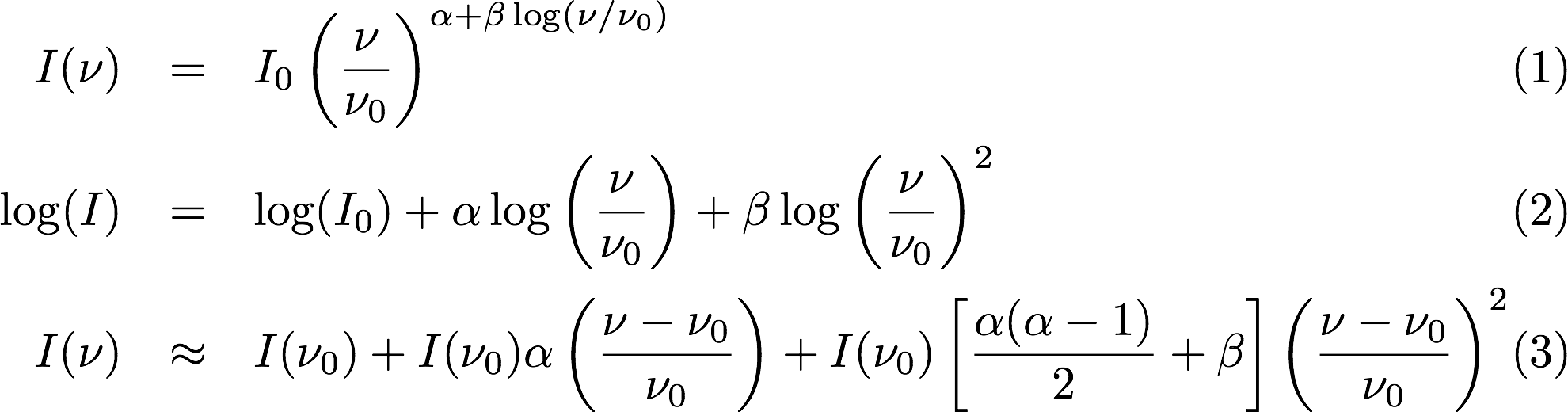
Equation 1 and 2 show the assumed spectral shape (in linear and log space respectively), while Equation 3 shows the Taylor expansion about the reference frequency (nu_0) for 3 terms. The coefficients of these terms are the quantities in the Taylor-term images: taylor 0 - a total intensity (I) image (at a fiducial frequency); taylor 1 - the alpha * I map, where alpha is the spectral index; taylor 2 - I * (beta + 0.5*alpha*(alpha-1)), where beta is the spectral curvature.

We want to extract a value for alpha & beta for each component. We do this by fitting to the total intensity image, as described above. Each resulting component is then fitted to the taylor 1 & 2 images, keeping the shape and location constant. This just fits the normalisation of the Gaussian. The total flux of the Gaussian is then extracted and used in the above relations.

The measurement of the spectral information in this way is dependent on the fitting, so one needs to request Gaussian fitting via the above parameters. The measurement of spectral index and spectral curvature can be requested independently (if, for instance, you have only a spectral index map).

Selavy defaults to assuming the images have been produced in the ASKAPsoft pipeline, and are thus named in a specific way. It is possible, however, to specify alternative names for the spectral index & curvature images (ie. Taylor 1 & 2 maps), although the data they hold must be formed in the same way (ie. conform to the above relationships). The image names are specified via the spectralTermImages input parameter. If this is not given, the names are derived, if possible, from the image name, assuming a standard format: if the total intensity image is named XXX.taylor.0.YYY, then the spectral index map will be XXX.taylor.1.YYY and the spectral curvature map will be XXX.taylor.2.YYY.

If the additional Taylor maps are not available, or the nterms parameter is set to a 1 or 2, then the values for spectral-index (when nterms = 1) and spectral-curvature (for nterms = 1 or 2) will be set to the special value of -99.

Measuring spectral terms from a cube¶

Selavy provides an alternative method for obtaining the spectral terms. If a cube is available (that is, a 3D image cube that preserves the individual channels, rather than collapsing them to form the Taylor images), then spectra can be extracted from it and the spectral terms determined via fitting. The cube need not have the same pixel grid - extraction is done based on the RA/Dec location.

Each component has its spectrum extracted in the same manner as for the Rotation Measure Synthesis (see below, and on Extraction of Spectra, Images and Cubelets). This spectrum is then fitted, using a non-linear Levenberg-Marquardt algorithm, with the function given by Equation 1 above. The user can select how many terms to fit - the default is 3, so that I_0, alpha and beta will be fit, but this can be set to 1 or 2 instead.

The user can also impose a threshold S/N value on a component-by-component basis, below which no fitting will be done. This defaults to zero, however, meaning all components will have their spectra fitted.

Thresholding the reporting of spectral terms¶

In both the taylor-term and cube-based methods, a threshold can be applied to either the peak flux or the peak signal-to-noise ratio, so that alpha & beta values for components below that threshold are not reported in the component catalogue. The calculations will still be performed, but the values will not be reported in the catalogue - the special value of -99 will be used instead.

Parameters for spectral term measurement¶

Parameter	Type	Default	Explanation
Selavy.spectralTermsFromTaylor	bool	true	Which mode to use to measure the spectral terms. True means use the Taylor-term images, while false means use a continuum cube.
Selavy.spectralTerms.threshold	float	none	Peak flux threshold for components, above which we report the spectral terms in the component catlaogue. If not given, then the thresholdSNR parameter will be used instead.
Selavy.spectralTerms.thresholdSNR	float	0.0	Peak signal-to-noise threshold for components, above which we report the spectral terms in the component catlaogue. The noise level here is the image noise
Selavy.spectralTerms.nterms	int	3	The number of terms to either use from Taylor-term images or to fit to in the component spectrum. Valid values are 1 (only I_0), 2 (I_0 &alpha), or 3 (I_0, alpha & beta). Larger values are set to 3, smaller values to 1.
Taylor-term images
Selavy.spectralTermImages	vector<string>	Derived from image name - see text	You can explicitly set the images for each term like so: spectralTermImages = [image1, image2].
Cube-based extraction
Selavy.spectralTerms.cube	string	“”	The name of the cube from which spectra should be extracted.
Selavy.spectralTerms.beamlog	string	“”	The name of the beamlog file, that describes how the PSF changes as a function of spectral channel.
Selavy.spectralTerms.snrThreshold	float		The threshold in component signal-to-noise ratio, below which no fitting is done to the spectra.

Rotation Measure Synthesis¶

Description of the algorithm¶

Selavy can be used to perform Rotation Measure Synthesis on the full-Stokes spectra of continuum components identified from a continuum map. The procedure follows that specified by the POSSUM survey science team, and can be described as follows:

A continuum component is found in a continuum image, and fitted with a 2D Gaussian (as described above).

Spectra are extracted from the corresponding location in Stokes I, Q, and U continuum cubes. The spectra are extracted from an NxN pixel box centred on the peak of the Gaussian (where N defaults to 5, as per the POSSUM specification). See Extraction of Spectra, Images and Cubelets for details on the method used.

The noise spectra in Q & U are extracted and averaged together to form the QU noise spectrum. This is used for weighting (if the “variance” weightType is selected).

The Q and U spectra are normalised by a model spectrum of Stokes I - we use either the Taylor-term expansion from the Stokes-I imaging or a low-order polynomial fit. They are then used to generate a Faraday Dispersion function (FDF) as a function of lambda-squared. The FDF is then multiplied by the model I flux at the reference wavelength.

The location of the peak of the FDF is recorded as the rotation measure of the component, with the peak value of the FDF (multiplied again by the Stokes I model spectrum) giving the polarised intensity.

The peak is also fitted with a three-point quadratic function, yielding a better estimate of the peak (avoiding the sampling of the Faraday depth function).

These and other quantities are written to a polarisation catalogue, that is named in the same way as the component and island catalogues - see the description above.

The extracted spectra of I, Q & U can also be written out to individual files, along with the FDF and RMSF arrays. These files can be either CASA or FITS format, selectable via the RMSynthesis.imagetype parameter. Unlike elsewhere, this defaults to fits. The FDF and RMSF files can each be written as either single complex-valued spectra, or separate spectra for the phase & amplitude. If FITS output is being used, the complex-valued option is not available. These files are not written for components with the polarised SNR below RMSynthesis.writeSpectra.polSNRthreshold.

Parameters for Rotation Measure Synthesis¶

Parameter	Type	Default	Explanation
Selavy.RMSynthesis	bool	false	Whether to run Rotation Measure Synthesis
Selavy.RMSynthesis.cube	string or vector<string>	“”	The name of the input cube to read the continuum spectra from. This can take wildcards (“%p”) for the polarisation or be a list of cubes corresponding to at least I,Q,U. See Extraction of Spectra, Images and Cubelets for more details.
Selavy.RMSynthesis.usefitstable	bool	false	If the imagetype is “fits” and this flag is set, the extracted spectra of each stokes are written to a binary table, along with the FDF and RMSF arrays.
Selavy.RMSynthesis.beamLog	string	“”	The filename of a beam log file (see Extraction of Spectra, Images and Cubelets) that can be used to correct the extracted fluxes with a channel-dependent beam. This can incorporate the “%p” wildcard.
Selavy.RMSynthesis.boxWidth	int	5	The width (N) of the NxN box to be applied in the extraction of Stokes spectra.
Selavy.RMSynthesis.noiseArea	float	50	The number of beam areas over which to measure the noise.
Selavy.RMSynthesis.robust	bool	true	Whether to use robust statistics in measuring the noise.
Selavy.RMSynthesis.writeSpectra	bool	true	Whether to write out the extracted spectra to image files on disk. This will also write out the FDF and RMSF determined from the RM Synthesis. The filenames are of the form [outputbase]_spec_[Stokes]_[objectID] for the spectra, [outputbase]_FDF_[objectID] for the FDF, and [outputbase]_RMSF_[objectID] for the RMSF.
Selavy.RMSynthesis.writeSpectra.polSNRthreshold	float	5	Threshold on the fitted polarised flux signal-to-noise ratio, below which the spectra listed above are not written.
Selavy.RMSynthesis.imagetype	string	casa	Type of image to create when extracting. Can be either “casa” or “fits” - anything else will throw an error.
Selavy.RMSynthesis.outputBase	string	“”	The base name for the output files - a front-end to extractSpectra.spectralOutputBase (Extraction of Spectra, Images and Cubelets).
Selavy.RMSynthesis.writeComplexFDF	bool	true	If true, write the FDF and RMSF spectra as single complex-valued image files. If false, the amplitude and phase of each are writtedn as separate files.
Selavy.RMSynthesis.weightType	string	variance	The type of weighting to be used in the RM Synthesis. Can be either “variance” (each channel is weighted by the inverse square of its noise), or “uniform” (each channel has a weight of 1). Anything else defaults to “variance”.
Selavy.RMSynthesis.modelType	string	taylor	The type of model used to represent the Stokes-I spectrum. This can be either “taylor”, in which case the Taylor-term parameters from the imaging & component fitting are used, or “poly”, in which case a low-order polynomial is used to model the spectrum.
Selavy.RMSynthesis.modelPolyOrder	int	3	The order of the polynomial to use in the Stokes-I model fit. Only used if modelType=poly.
Selavy.RMSynthesis.numPhiChan	int	40	Number of channels in the Faraday depth sampling vector.
Selavy.RMSynthesis.deltaPhi	float		Spacing between the Faraday depth channels [rad/m2].
Selavy.RMSynthesis.phiZero	float		Centre RM of the Faraday depth vector, [rad/m2].
Selavy.RMSynthesis.polThresholdSNR	float		Signal-to-noise threshold (in the FDF) for a valid detection.
Selavy.RMSynthesis.polThresholdDebias	float		Signal-to-noise threshold (in the FDF) above which to perform debiasing.

Spectral extraction for components¶

Description¶

Selavy is able to extract spectra from a spectral cube for each component brighter than a nominated flux level. These spectra can be either source spectra (from an NxN box centred on the comoponent location) or noise spectra (in the same manner as above).

The flux level is applied to the integrated flux of the component. Comopnents brighter than the nominated flux level are extracted using the methoeds described in more detail on Extraction of Spectra, Images and Cubelets. The flux limit value should be given in mJy (the units used in the component catalogue).

For source spectra, the parameters shall have the prefix Selavy.Components.extractSpectra, and have available all parameters in the “Spectral extraction” section of Extraction of Spectra, Images and Cubelets. In addition, there are these two parameters:

Parameter	Type	Default	Explanation
Selavy.Components.extractSpectra	bool	false	Whether to run the spectral extraction for components
Selavy.Components.extractSpectra.fluxLimit	float		The flux limit to apply to the integrated fluxes of components. Only those brighter than this level (in mJy) will be extracted.

Similarly, for noise spectra, the parameters shall have the prefix Selavy.Components.extractNoiseSpectra, and have available all parameters in the “Noise Spectra” section of Extraction of Spectra, Images and Cubelets. In addition, there are these two parameters:

Parameter	Type	Default	Explanation
Selavy.Components.extractNoiseSpectra	bool	false	Whether to run the noise spectra extraction for components
Selavy.Components.extractNoiseSpectra.fluxLimit	float		The flux limit to apply to the integrated fluxes of components. Only those brighter than this level (in mJy) will be extracted.