Spectroscopic Parallax
The term spectroscopic parallax is a misnomer as it actually has nothing to do with parallax. It is, however, a way to find the distance to stars. Most stars are too far away to have their distance measured directly using trigonometric parallax but by utilising spectroscopy and photometry an approximate distance to them can be determined. Let us see how this works.
- If we take a spectrum of a star we can determine:
- Its spectral class.
- Its luminosity class.
- Using photometry we can measure the apparent magnitude, m, mV or V for the star.
- If we use B and V filters we can also determine the blue apparent magnitude, B and thus determine the star's colour index, CI = B - V.
- Knowing either the star's spectral class or colour index allows us to place the star on a vertical line or band along a Hertzsprung-Russell Diagram. If we also know its luminosity class we can further constrain its position along this line, that is we can distinguish between a red supergiant, giant or main sequence star for example.
- Once we know its position on the HR diagram we can infer what its absolute magnitude, M should be by either reading off across to the vertical scale of the HR diagram or looking it up from a reference table. A main sequence (luminosity class V) star with a colour index of 0.0 (ie A0 V) has an absolute magnitude of +0.9 for example.
- Now knowing m from measurement and inferring M we can use the distance modulus equation:
m - M = 5 log(d/10) (4.2)
to find the distance to the star, d, in parsecs.
In practice this technique is not very precise in determining the distance to an individual star. Uncertainties in the absolute magnitude of stars of specific spectral and luminosity class range from about 0.7 up to 1.25 magnitudes. These then give a factor of 1.4 to 1.8 × variation in the resultant distance. Nonetheless it is still an important methods for estimating distance to stars beyond direct trigonometric parallax measurement.
Example of Spectroscopic Parallax Calculation:
γ Crucis is an M3 III star with a measured value of mV = 1.63 and a colour index of +1.60. This means that it is a red giant. Plotting its position on the HR diagram below we can estimate its absolute magnitude to be about -0.8. In fact if we look up a standard reference table we find the the absolute magnitude for a III luminosity class star with a colour index of +1.60 is -0.60.
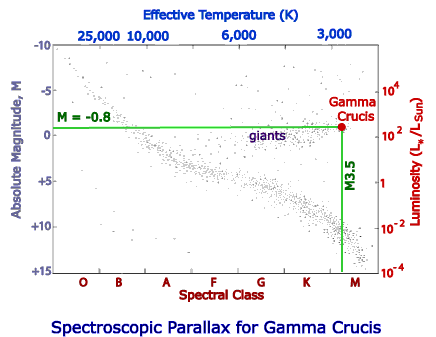
Now if we use the tabulated value of M = -0.60 with the distance modulus equation (4.2) we have:
which can be written as:
now substituting in:
so &gamma Crucis is about 28 pc distant which is within 1 pc of the published Hipparcos value. If we used the graphically obtained estimate value of M ≈ -0.8 then:
so γ Crucis would have a value of about 31 pc distance, about a 15% error.
Although this method is not accurate for individual stars, if carried out for many stars it can yield statistically useful values.
