Luminosity and the Distance to Stars
Luminosity and Brightness
Stars vary in their effective temperature and colour. A hot star radiates more energy per second per metre surface area than a cooler star. Does this then mean that a hot star is going to appear brighter to us than a cooler one? The answer to this actually depends on a few factors. These include:
- The size of a star. If two stars have the same effective temperature but differ in size then the larger star has a greater surface area and as it radiates the same amount of energy per unit surface area per second as the smaller star its total power output or luminosity must be greater.

- The distance to the star. All the stars we see in the night sky are at vast distances from us but some are much closer relatively than others. For two stars of identical size and temperature, the closer one to us will appear brighter. An analogy is a row of street lights, the closer ones appear much brighter than those in the distance.
- Intervening matter. Contrary to common belief interstellar space is not a perfect vacuum. Dust and gas between stars can absorb and scatter starlight leading to a reduction in brightness and a reddening in colour.
The total energy output per second of a star is called its luminosity, L, sometimes written as L*. Our Sun's luminosity is about 3.84 × 1026 W. Rather than use absolute values it is often convenient to compare the luminosity of a star, L* to that of the Sun so that for instance it may be 1,000× LSun. The source of energy in stars is described on another page.
Stars vary enormously in luminosity, ranging from less than 10-4 × that of our Sun to 106 × more luminous.
What is the relationship between distance to a star and its brightness (that is the intensity of light we receive from it)? As we can see in the diagram below as we move away from a star the radiation it emits has to cover a greater surface area. Imagine a sphere at a distance r from the star. Assuming a star is spherical and emits radiation equally in all directions the intensity of the energy at distance r over an area A will be I. If we double the distance from the star to 2r this same amount of energy is now distributed over four times the surface area, that is 4A. This means that the intensity per unit A is only ¼ the amount at r. At 3× the distance it will only be 1/9th the intensity per unit A and so forth.
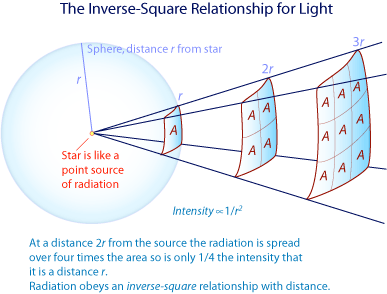
This relationship for light (or any electromagnetic radiation) is called an inverse-square relationship.
If we have two identical stars but one is 10× further away than the other the more distant star will appear 1/102 or only 1/100 times as bright as the closer one.
Distances to the Stars
To quote Douglas Adams from The Hitchhiker's Guide to the Galaxy;
“Space is big ... very big”
Distances in space are so vast they are hard for us to comprehend. Astronomers can measure the distance to the nearest stars using a method known as trigonometric parallax. This gives a distance to Alpha (α)Centauri, the nearest star system to us other than our Sun, of about 4.1 × 1016 m. The metre is not really a useful unit for such a large number. Astronomers actually use a unit of distance called the parsec (pc) to express distances to other stars and galaxies. One parsec is about 3.09 × 1016m so α Cen is about 1.3 parsecs distant. This is also equal to about 4.3 light years.
A light year is simply the distance that light travels in a vacuum in one Earth year (9.46 × 1015m). One parsec = 3.26 light years. All the stars visible to the unaided eye in the night sky are relatively bright stars in our local region of the Milky Way. Most stars are too far away to have their distance determined by trigonometric parallax so other methods have to be employed. (More details about how distances to stars are determined can be found in the Option 9.7 Astrophysics sections on astrometry and spectroscopic parallax). The Milky Way itself is about 35,000 parsecs (or 35 kpc) across. The nearby satellite galaxy, the Large Magellanic Cloud is about 50 kiloparsecs distant. At the cosmological scale, the distance to most galaxies is measured in megaparsecs (millions of parsecs).
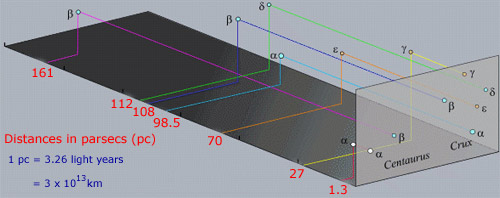
If we look at the region around the constellation Crux (the Southern Cross) in the night sky we see several bright stars. A long exposure photograph or CCD image reveals many more as shown below.

In the above image, α Cen (for Centaurus)appears slightly brighter than β Cen which in turn appears much brighter than ε Cru. Johannes Bayer in his 1603 catalogue introduced the idea of labelling the brightest apparent star in a constellation as α, the next brightest β and so on through the 24 letters of the Greek alphabet. When we determine the distance to each of the bright stars in Crux however we see that their distances vary greatly. α Cen is only 1.3 parsecs away whereas β Cen is 161 pc distant. Given that it appears only slightly dimmer than α Cen in the night sky this means that β Cen is intrinsically far more luminous.