Medieval & Renaissance Astronomy
Medieval Astronomy
Contrary to common misconception the period between the end of the classical era and the start of the Renaissance was not devoid of scientific progress. Islamic scholars translated many of the surviving writings from Greek or Syriac into Arabic from the late 700's onwards. These translations in turn were transported into Islamic Spain where they eventually fell into Christian hands and were translated into Latin. Islamic astronomers such as Muhammad al-Battani (c. 850 - 929) refined Ptolemy's model and their published works and tables were later used by Western astronomers. Even today the influence of Islamic astronomers is found in the names of many of the bright stars such as Betelgeuse (α Ori), Alnitak (ζ Ori) and Zubenelgenubi (α Lib).

As Western scholars studied the Latin translations of the classical philosophers they incorporated many aspects of their work into the prevailing theology and world view. Aristotle's physics described the motion of objects and the refined model of Ptolemy was used to study the night sky. The Frenchman, Nicole Oresme (1320 - 82) applied an early concept of the centre of gravity, used mathematics to argue against astrology and even suggested the existence of other inhabited worlds in space. Nicolas of Cusa (born c. 1401) supported this idea and rejected the concept of a static Earth at the centre of all motions.
Georg Puerbach (1423 - 61) refined the Almagest and wrote a popular textbook on it. This prompted a renewal of interest in the need for accurate observations. His pupil, Regiomontanus (1436 - 76) highlighted problems with Ptolemy's work based on observations made at his purpose-built observatory. He published his own and other writings on astronomy and the increasing availability of printed books did much to spread ideas among scholars. In 1482 he observed a bright comet that was later identified as one of the visits of Comet Halley and was most likely working towards a heliocentric model influenced by Aristarchus at the time of his death.
The Renaissance
Nicolaus Copernicus (1473 - 1543)

Copernicus studied classics and mathematics at Krakow in his native Poland, canon law in Bologna and Ferrara and medicine at Padua in Italy. His keen interest in astronomy was fostered in Italy and developed back in Poland where he was canon at the cathedral in Frauenberg (now Frombeck) where he spent most of his life.
A conjunction of Jupiter and Saturn in 1504 was observed to differ by 10 days from the predictions of tables based on Ptolemy's work. This, combined with Copernicus' abhorrence of the equant drove him to develop an improved model. Influenced by the work of Regiomontanus (thus also Aristarchus) and neoplatonism (which viewed the Sun as the Godhead and source of all knowledge) he produced his own model. He withheld publication due to his conservative nature and fear of ridicule but was eventually persuaded by Rheticus. Allegedly he received the first copy of his work De revolutionibus orbium (On the revolution of the heavenly spheres) on his deathbed in 1543.
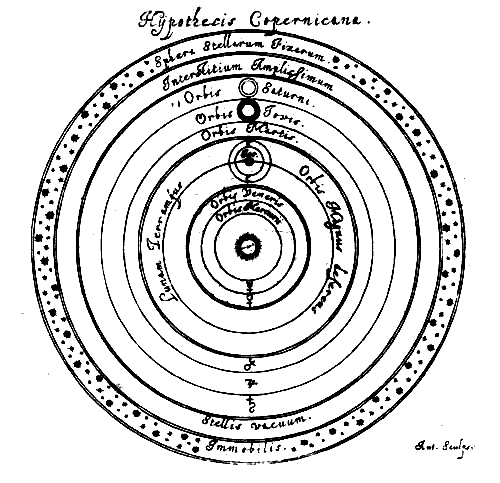
In Copernicus' model a spherical Earth rotates daily on it axis whilst it and the other planets each orbit the Sun. The period of the planets' orbits increases with increasing distance from the Sun. The Sun was not exactly at the centre of the planetary orbits thus strictly speaking the model is heliostatic rather than heliocentric.
There were several advantages of Copernicus' model over that of Ptolemy:
- It could predict planetary positions to within 2°, the same as that of Ptolemy.
- Retrograde motion of planets was explained by the relative motion between them and the Earth.
- Distances between planets and the Sun could be accurately determined in units of the Earth-Sun distance (ie Astronomical Units).
- Orbital periods could be accurately determined.
- It explained the difference between the inferior planets (Mercury and Venus) that were always observed close to the Sun and the superior ones (Mars, Jupiter and Saturn).
- It preserved the concept of uniform circular motion without the need for equants.
- It preserved Aristotle's concept of real spheres nestled inside one another.
- Unlike Ptolemy's model it did not require the Moon to change in size.
Copernicus' model also had several problems which contributed to its failure to immediately supplant Ptolemy's model:
- No annual stellar parallax could be detected. Copernicus explained this as due to the fact that the stars were a vast distance hence any parallax would be very small and difficult to detect.
- It required a moving Earth, This would contradict Aristotelian physics and Copernicus presented no new laws of motion to replace Aristotle.
- By removing the Earth from its natural place it was philosophically and theologically unacceptable to many scholars.
- It was no more accurate than Ptolemy's in predicting planetary positions.
- It was actually more complicated then Ptolemy's model. In his efforts to avoid the equant but retain uniform circular motion he had to introduce more devices to fit his observations.
Tycho Brahe (1546 - 1601)

Tycho Brahe, of Danish noble stock, was probably the greatest astronomical observer of the pre-telescope era. Early observations in the 560's revealed inaccuracies with existing tables and spurred him onto making systematic, long-term observations and records. This task would occupy the rest of his life. With generous funding from the King of Denmark he established a dedicated observatory, Uraniborg, on the island of Hven (now Ven). He built large instruments such as quadrants from wood and brass that improved on earlier designs. The measurements he made were up to ten times more accurate than any preceding ones and were at the limit of that obtainable by the unaided eye. The investment by the Danish King amounted to 5% of his total income, still a record for investment on scientific research. Brahe eventually fell out with the Danish court and moved to Prague for his final years.
In November 1572 a new star appeared in the constellation Cassiopeia. Brahe's observations showed that it was motionless relative to nearby stars suggesting to him that it was in fact a star and not a tail-less comet. Five years later he observed a bright comet and discerned no parallax and placed it at least six times further from Earth than the Moon. Both of these observations challenged the Aristotelian orthodoxy. The stars were supposed to be changeless and perfect whilst comets were supposed to be confined to the sub-lunary sphere, that is between the Earth and Moon. Further observations revealed that the comet would move through the solid crystalline spheres of an Aristotelian Universe.

To reconcile his observations with his philosophy Brahe developed his own model, incorporating some aspects of Copernicus' but rejecting the idea of a moving Earth. Although his hybrid model enjoyed a brief period of popularity it was soon replaced by the work of his assistant, Johannes Kepler.
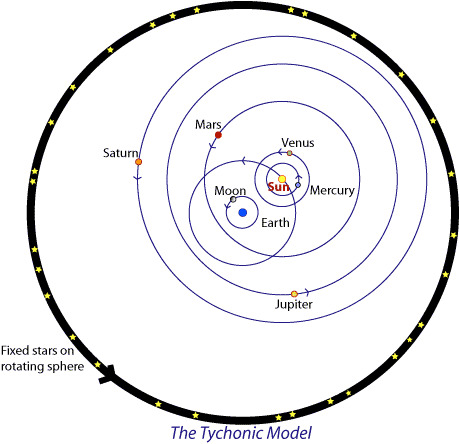
Brahe's model was somewhat of a hybrid and drew upon Herakleide's earlier concepts. It had a static Earth at the centre of the Universe with the Moon orbiting it. A rotating sphere of fixed stars also revolved around the Earth once every 24 hours. The planets however orbited about the Sun which itself orbited the Earth. It utilised epicycles, deferents and equants. In his model there is no need for stellar parallax. The diagram above shows a simplified representation.
Brahe's lasting legacy was his long-term and meticulous observations of planetary motions, especially those of Mars. This data was used after his death by Kepler, who worked as his assistant during Brahe's last year.
Johannes Kepler (1571 - 1630)

Best known for his key works on astronomy, Johannes Kepler made valuable contributions in other fields. In his works on optics he examined the refraction of light, correctly explained the working of the eye for the first time and provided a theoretical basis for telescopes with suggested means of improving them. His explanation on the new Napierian logarithms did much to encourage their wide acceptance. Given a challenge to calculate volumes of wine casks he ended up developing an approach to infinitesimal calculus well ahead of the ideas of Liebniz and Newton. Kepler had studied under the renowned astronomer Michael Maestlin, one of the first proponents of Copernicus' work.
In his first astronomical work, Mysterium cosmographicum (The cosmic mystery) in 1596, Kepler upheld his belief in the Copernican system. He also discovered a geometrical relationship for the orbits of the planets around the Sun. Between the sphere of each planet's orbit he found he could place one of the five regular solids, for example a cube between Jupiter and Saturn, so that the six planets were separated by five regular solids. This system reflects the influence on Kepler of the Platonic-Pythagorean tradition of matching order in nature with the regularities of mathematics. Of greater long-term importance however was his suggestion that the Sun somehow affected the orbits of the planets, perhaps by magnetism.
Kepler tried to fit Brahe's data to the Copernican model but consistently arrived at errors of at least eight seconds of arc, small but not insignificant. He was finally forced to abandon the concept of uniform circular orbital paths but it was to take him several years of painstaking, methodical calculations before he arrived at an alternate model that fitted Brahe's 20 years of data on Mars. The results were published in 1609 in his work Astronomica nova (New Astronomy). In it he explained what are now known as his first two laws of planetary motion.
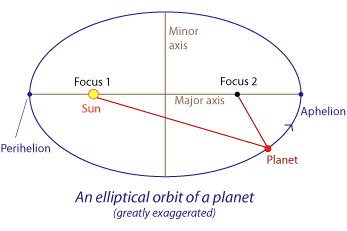
All planets orbit the Sun in elliptical orbits with the Sun as one common focus. Note the eccentricity of the ellipse has been greatly exaggerated in the above diagram. For most planets their orbits are almost circular.
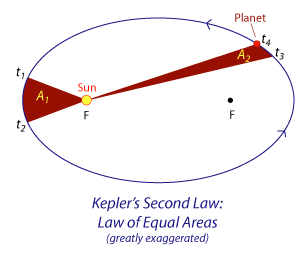
The line between a planet and the Sun (the radius vector) sweeps out equal areas in equal periods of time.
In the diagram, the time interval t2-t1 = t4-t3 so the areas swept through in equal times are equal,
that is A1 = A2.
This effect is very noticeable in comets such as Comet Halley that have highly elliptical orbits. When in the inner Solar System, close to the Sun at perihelion, they move much faster than when far from the Sun at aphelion.
Kepler actually formulated the law of equal areas first and it then led him to the law of ellipses. His third law was not published until 1618 in Harmonice mundi (The Harmony of the World). This resulted from his attempts to find a relationship between the distance of a planet from the Sun and its orbital period.
Kepler's Third Law: The Law of Periods or the Harmonic Law*.
The square of a planet's period, T, is directly proportional to the cube of its average distance from the Sun, r.
Mathematically this can be expressed as:
or T2/r3 = k (1.1)
where k is a constant and the same for all planets or orbital bodies (such as comets) in a given system.
If T is measured in Earth years and r in astronomical units (AU) then for the Earth, T = 1 and r = 1 so:
∴ 1/1 = k
ie. k =1
(* Note this equation is not explicitly required for 8.5 The Cosmic Engine unit in the NSW Preliminary Course. It is, however, explicitly required in Unit 9.2 Space in the HSC course.)
The implication of Kepler's Third Law is that planets more distant from the Sun take longer to orbit the Sun. Let us see how this can be used to determine the mean distance of Mars from the Sun if its orbital period is 1.88 Earth years.
Then rewriting for r
r3 = T2/k
r = ((1.88)2/1)1/3
so r = 1.524 AU
So Mars is 1.524 astronomical units from the Sun.
Kepler's laws of planetary motion were empirical, they could predict what would occur but could not account for why planets behaved in such a manner. His Rudolphine tables of planetary motion published in 1627 were more accurate than nay previous ones. He came close to uncovering the concept of gravitation and corresponded with Galileo and was aware of his telescopic discoveries.
