The Magnitude Scale
- Historical Background
- Apparent Magnitude, m
- Absolute Magnitude, M
- Finding the Distance to Stars - Distance Modulus
- Magnitude/Distance Calculations
- Naming & Identifying Stars
Study the star field photograph shown below. It shows a region of the sky around the constellation Crux, commonly called the Southern Cross. Move your cursor across the photo to identify some stars.
Which star is brightest?

If you answered Alpha (α) Centauri, the star at the bottom left of the photograph you are right. As you can see, a photographic image such as this shows many more stars than you can see with your unaided eye. Nonetheless some stars are more prominent than others. In choosing α Centauri you made some assumptions. What were they?
A photograph such as this shows bright stars as larger disks than fainter stars. Does this mean that these stars are physically larger than the fainter stars in the photo? Remember, in the section on astrometry we learnt that all stars other than our Sun are so distant that they are effectively point sources. Why then do some appear brighter (to our eyes) or larger (in photographs) than others? What, in fact is brightness and how can we measure it? The answers to these questions form the focus of this section.
Historical Background

The concept of measuring and comparing the brightness of stars can be traced back to the Greek astronomer and mathematician Hipparchus (190 - 120 BC). One of the greatest astronomers of antiquity, he is credited with producing a catalogue of 850 stars with positions and comparative brightnesses. In his system, the brightest stars were assigned a magnitude of 1, the next brightest magnitude 2 and so on to the faintest stars, just visible to the unaided eye which were magnitude 6. This six-point scale can be thought of as a ranking, first-rate stars, the brightest, were first magnitude and dim low-rate stars were sixth magnitude.
The discovery of fainter stars with telescopes in the early 1600s required the scale to be extended beyond magnitude 6. The development of visual photometers, instruments to measure stellar intensities, in the nineteenth century by John Herschel and others prompted the need for astronomers to adopt an international standard. The fact that eyes detect differences in intensity logarithmically rather than linearly was discovered in the 1830s. In 1856 Norman Pogson proposed that a star of magnitude 1 was 100 × brighter than a star of magnitude 6. A difference of one magnitude was therefore equal to 5√100 = 2.512 times in brightness.
Apparent Magnitude, m
The apparent magnitude, m, of a star is the magnitude it has as seen by an observer on Earth.
A very bright object, such as the Sun or the Moon can have a negative apparent magnitude. Even though Hipparchus originally assigned the brightest stars to have a magnitude of 1 more careful comparison shows that the brightest star in the night sky, Sirius or α Canis Majoris (CMa) actually has an apparent magnitude of m = -1.44. With the recalibration of Hipparchus' original values the bright star Vega is now defined to have an apparent magnitude of 0.0.
Following the telescopic discovery of faint stars in the early 1600s the magnitude scale has also had to be extended to objects fainter than magnitude 6. The table below shows the range of apparent magnitudes for celestial objects.
| Object | Apparent Magnitude |
|---|---|
| Sun |
-26.5
|
| Full Moon |
-12.5
|
| Venus |
-4.3
|
| Mars or Jupiter |
-2
|
| Sirius (α CMa) |
-1.44
|
| Vega (α Lyr) |
0.0
|
| Alnair (α Gru) |
1.73
|
| Naked-eye limit |
6.5
|
| Binocular limit |
10
|
| Proxima Cen |
11.09
|
| Visual limit through 20 cm telescope |
14
|
| QSO at redshift z = 2 |
≈ 20
|
| Cepheid in galaxy M100 observed with HST |
26
|
| Galaxy at z = 6 observed with Gemini 8.1 m telescope |
28
|
| Limit for James Webb Space Telescope |
≥ 30
|
If a star of magnitude 1 is 2.512 × brighter than a star of magnitude 2 and 100 × brighter than a sixth magnitude star how much brighter is it than a star of magnitude 3? You need to be careful here. It is not simply 2 × 2.512 different. You need to remember that a difference of one magnitude equals 5√100 = 2.512. A difference of 2 magnitudes therefore = 2.5122 = 6.31 × difference in brightness.
Two objects of different magnitudes therefore vary in brightness by 2.512 raised to the power of thee magnitude difference. If we write this as an equation, the ratio of brightness or intensity, IA/IB between two objects, A and B, with magnitudes mA and mB is given by the following equation:
Let us have a look at an example.
Example 1: Comparing two stars.
How much brighter is Alnair, apparent magnitude of +1.73 than Proxima Cen with a magnitude of 11.09?
Using equation 4.1 we have:
so, substituting in:
Example 2: How much brighter is the Sun than the full Moon?
For this we recall from the table above that the Sun has an apparent magnitude of -26.5 and the full Moon, - 12.5.
So using equation 4.1 we get:
substituting in gives us:
It is important to remember that magnitude is simply a number, it does not have any units. The symbol for apparent magnitude is a lower case m; you must make this clear in any problem.
Absolute Magnitude, M
What does the fact that Sirius has an apparent magnitude of -1.44 and Betelgeuse an apparent magnitude of 0.45 tell us about these two stars? Another way of thinking about this is to ask why is Sirius the brightest star in the night sky? A star may appear bright for two main reasons:
- It may be intrinsically luminous, that is it may be a powerful emitter of electromagnetic radiation, or
- It may be very close to us, or both.
The apparent magnitude of a star therefore depends partly on its distance from us. In fact Sirius appears brighter than Betelgeuse precisely because Sirius is very close to us, only 2.6 pc away whereas Betelgeuse is about 160 pc distant. The realisation that stars do not all have much the same luminosity meant that apparent magnitude alone was not sufficient to compare stars. A new system that would allow astronomers to directly compare stars was developed. This system is called the absolute magnitude, M.
The absolute magnitude, M, of a star is the magnitude that star would have if it were at a distance of 10 parsecs from us. A distance of 10 pc is purely arbitrary but now internationally agreed upon by astronomers. The scale for absolute magnitude is the same as that for apparent magnitude, that is a difference of 1 magnitude = 2.512 times difference in brightness. This logarithmic scale is also open-ended and unitless. Again, the lower or more negative the value of M, the brighter the star is. Absolute magnitude is a convenient way of expressing the luminosity of a star. Once the absolute magnitude of a star is known you can also compare it to other stars. Betelgeuse, M = -5.6 is intrinsically more luminous than Sirius with an M = 1.41.
Our Sun has an absolute visual magnitude of 4.8.
Finding the Distance to Stars - Distance Modulus
As you may recall from the section on astrometry, most stars are too distant to have their parallax measured directly. Nonetheless if you know both the apparent and absolute magnitudes for a star you can determine its distance. Let us look again at Sirius and Betelgeuse plus another star called GJ 75.
| Star | apparent magnitude m |
Absolute magnitude M |
Distance Modulus m - M |
|---|---|---|---|
| Sirius |
-1.44
|
1.41
|
-2.85
|
| Betelgeuse |
0.45
|
-5.14
|
5.59
|
| GJ 75 |
5.63
|
5.63
|
0.00
|
How far away is GJ 75? It is an unusual star in that its apparent and absolute magnitudes are the same. Why? The reason is that it is actually 10 parsecs distant from us, so by definition its two magnitudes must be the same.
What about Sirius? Its apparent magnitude is lower (therefore brighter) than its absolute magnitude. This means that it is closer than 10 parsecs to us. Betelgeuse's apparent magnitude is higher (therefore dimmer) than its absolute magnitude so it would appear even brighter in the night sky if it were only 10 parsecs distant.
Is there a quick way of checking whether a star is close or not? Looking at the above table we see that if a star is at a distance of 10 parsecs, then m = M or m - M = 0. For Sirius, m - M = (-1.44) - 1.41 = -2.85. This value is negative and Sirius is closer than 10 pc. For Betelgeuse, m - M = 0.45 - (-5.14) = 5.59. This value is positive and Betelgeuse is more than 10 pc distance.
Astronomers use the difference between apparent and absolute magnitude, the distance modulus, as a way of de terming the distance to a star.
- Distance Modulus = m - M.
- Distance modulus is negative for stars closer than 10 parsecs.
- Distance modulus is positive for stars further away than 10 parsecs.
- The size of the distance modulus determines the actual value of the distance, so that a star of distance modulus 1.5 is closer than one with a distance modulus of 8.7.
Magnitude/Distance Calculations
The distance modulus can be used to determine the distance to a star using the equation:
where d is in parsecs. Note that if d = 10 pc then m and M are the same. (A formal derivation of this equation is given in the next page on luminosity). The NSW HSC Syllabus Formula Sheet provides the equation as:
but this is simply a reworking of equation 4.2. You should be comfortable in solving this equation given any two of the three variables. Let us know look at how you can solve some examples.
Example 3: Given m and d, need to find M.
β Crucis (or Mimosa) has an apparent magnitude of 1.25 and is 108 parsecs distant. What is its absolute magnitude?
Using equation 4.3 we have:
so β Crucis has an absolute magnitude of -3.92
Note this calculation has shown full working so that each step is explicit. (Remember in solving magnitude equations log refers to logarithms to base 10 and not natural logarithms or ln.)
Example 4: Given m and M, find d.
Betelgeuse has an apparent magnitude of 0.45 and an absolute magnitude of -5.14. How far away is it?
This problem requires us to rewrite equation 4.2 to give us d as the unknown. This is shown below:
which can be written as:
now substituting in:
so Betelgeuse is about 130 pc distant.
Again, this example shows complete working whereas in reality you may not show every step. It is important, however, that you set your working to such problems out clearly so you can check your algebraic manipulation and your substitutions. Working with logs and indices can be tricky so ensure you know how to do these on your calculator.
Example 5: Given M and d, find m.
In practice this type of problem is less realistic for actual objects as we can normally measure their apparent magnitudes directly however it may be that we wish to calculate what apparent magnitude a class or type of object may have given the other parameters. Again, starting with equation 4.3 let us determine how bright a supergiant such as Deneb with an absolute magnitude of -8.73 would appear if it was 230 parsecs away.
so substituting in:
so Deneb would have an apparent magnitude of -1.89. This would make it brighter in our night sky than Sirius (m = -1.44). In reality Deneb is about 990 pc distant although this value has a large uncertainty.
Example 6: What if d is not given but parallax, p is given?
This is actually very straight forward. Recall from the section on astrometry that there is a direct relationship between distance and parallax.
so you simply need to insert this into equation 4.2 or 4.3.
Naming & Identifying Stars
Let us know revisit that photo of Crux and the Pointers from the top of this page. The photo below shows the same region with the prominent stars labelled. They also have their apparent magnitudes shown. Crux is a constellation, one of 88 regions that the celestial sphere has been broken up into and agreed upon internationally by astronomers. Crux is actually the smallest of the constellations and is easily identified in the southern skies. The prominent nearby stars commonly called the Pointers are actually part of a large constellation called Centaurus.

Now you may notice that the stars are named using letters from the Greek alphabet; α, β, γ δ and ε (alpha, beta, gamma, delta, epsilon being the first five) followed by the standard three-letter abbreviation for each constellation (Cru for Crucis or Crux and Cen for Centaurus). If you look closely at the apparent magnitudes for the five named stars in Crux you will see that the brightest star is labelled α, the next β and so on. This system is called the Bayer system, after Johann Bayer who introduced it in 1603. The brightest star in a constellation is assigned the letter α, the next β and so on. An exception to this rule is &alpha Orionis or Betelgeuse. It is in fact fainter than β Ori, Rigel by a small amount. This is an interesting historical case solved by the realisation that Betelgeuse has dimmed slightly in brightness since it was named under the Bayer system.
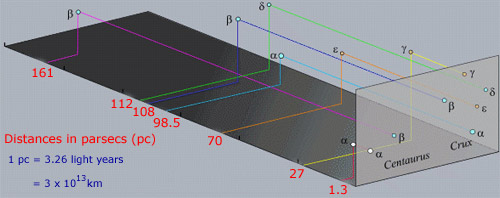
One point to remember about constellations is that the stars within a constellation are not usually physically associated with each other, unlike stars in clusters. The fact that appear close together is purely an alignment effect along tour line of sight. In fact, the stars in the region above are widely separated in distance from us as shown in the next image.
Some of the bright stars such as α Cen also have their own specific name. Sirius (α CMa) is one such examples whilst α Cen is also called Rigel Kentaurus. Many star names are Arabic in origin from the era when Greek records were preserved and developed by Islamic astronomers. The problem with the Bayer system of naming stars is that there are only 24 letters in the Greek alphabet but there are many more stars than is in each constellation.
Most stars in fact do not have a specific name or Bayer classification. These days astronomers have compiled vast catalogs of stars, some with over 10 million objects, so most stars only have a catalog number. Stars may have many more than one identification name or catalog number, depending on the number of catalogs they are in. The variable star, δ Cep for example is also known as HIP 110991, SAO 34508, or any of more than 30 other identifiers! Many catalogs utilise celestial coordinates such as Right Ascension and Declination to identify objects. Thus δ Cep is known as IRAS 22273+5809, CCDM J22292+5825A and AAVSO 2225+57. The slight variations in RA and dec for the catalogs arises due to the proper motion of the stars and the precession of the reference frame.