The first double pulsar
|
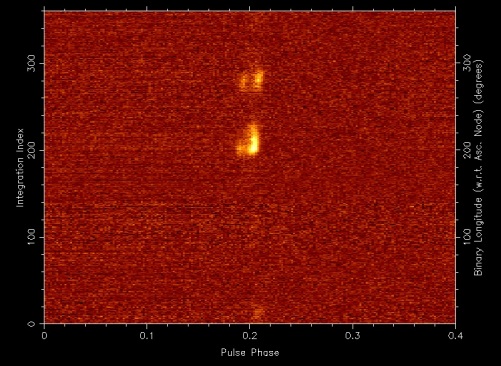
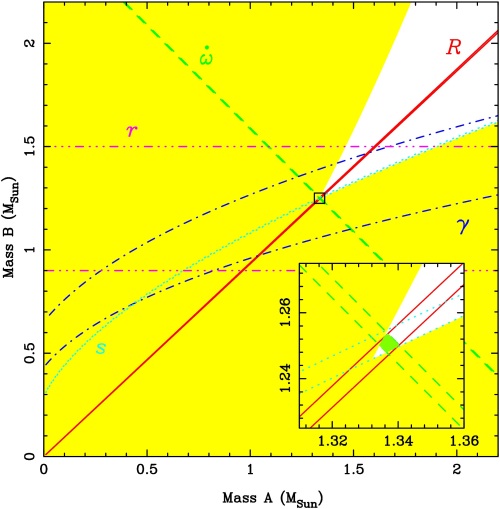
R. N. Manchester on behalf of the Parkes High-Latitude Pulsar Survey team: M. Burgay (University of Bologna, Italy); F. Camilo (Columbia University, USA); N. D'Amico (Cagliari Astronomical Observatory, Italy); P. C. C. Freire (Arecibo Observatory, Puerto Rico); B. C. Joshi (GMRT, India); M. Kramer (University of Manchester, UK); D. R. Lorimer (University of Manchester, UK); A. G. Lyne (University of Manchester, UK); M. A. McLaughlin (University of Manchester, UK); R. N. Manchester (ATNF); A. Possenti (Cagliari Astronomical Observatory, Italy); J. Reynolds (ATNF) and J. Sarkissian (ATNF) Pulsars have a history of new and unexpected developments - think of the first period glitch, the first binary pulsar and the first millisecond pulsar. These and other similar discoveries have had profound and wide-ranging implications, impacting not only on pulsar astrophysics, but also on stellar evolution, gravitational physics, astrometry and many other areas. This tradition has continued with the discovery of the first-known double-pulsar system at Parkes. Beginning with the famous Hulse-Taylor binary pulsar (PSR B1913+16), it has been known for a long time that in some binary systems the companion, as well as the pulsar, is a neutron star. Only five or six of the 80 or so previously known binary pulsars are believed to be double-neutron-star systems and, despite careful searches, in no case had the second neutron star been detected as a pulsar. This is not too surprising as the second-born pulsar has a much shorter lifetime than the first, which in all known systems has been recycled to form a rapidly spinning and weakly magnetised pulsar. This story begins with the discovery of a 22-millisecond pulsar, PSR J0737-3039, by Marta Burgay, a University of Bologna student working with the Parkes High-Latitude Pulsar Survey team. This survey uses the Parkes multibeam receiver to search a region of sky in the third Galactic quadrant extending between latitudes of -60° and +60°. It was immediately clear that PSR J0737-3039 was a member of a binary system, which subsequent observations showed to have a period of only 2.4 hours. Furthermore, the amplitude of the Doppler shifts showed that the companion was massive and probably another neutron star. With a mean orbital velocity of 0.1 per cent of the velocity of light, this is the most relativistic binary pulsar known and many relativistic perturbations of the observed pulsar period are expected to be detectable. Indeed, the relativistic precession of periastron was observed in just a few days, implying that the sum of the masses of the two stars is about 2.59 solar masses. One of the most interesting aspects of this system is that it raises the predicted rate of detections of double-neutron-star mergers by gravitational wave detectors such as LIGO by nearly an order of magnitude. These results were published in Nature by Burgay et al. in December 2003. Figure 1 shows an artist's impression of the two pulsars. These results were very exciting, but this system had more surprises in store. While testing a pulsar search program on a Parkes observation of this pulsar, Duncan Lorimer was astounded to see a very strong signal at a period of 2.78 s with a dispersion measure equal to that of the 22-ms pulsar. Further investigation showed that this signal had the inverted Doppler shifts of the 22-ms pulsar. There was no doubt that it was the neutron-star companion the first time that the second neutron star in such a system had been seen as a pulsar! The emission from this pulsar, PSR J0737-3039B, is strongly modulated with orbital phase and only bright for two 10-minute intervals during the 2.4-hour orbit. At the time of the discovery-observation of the A pulsar, the B pulsar was turned off! The discovery of the B pulsar was announced in Science Express on 8 January 2004 and published in Science in the 20 February 2004 issue (Lyne et al. 2004). Figure 2 shows the orbital modulation of the B pulsar signal. This figure shows that not only is the pulse amplitude varying with orbital phase, the pulse shape is also changing! Such modulation is unprecedented in pulsar astronomy, and is very likely due to the relativistic wind from the A pulsar penetrating deep into the magnetosphere of the B pulsar. Back-of-the-envelope calculations suggest that more than 90 per cent of the B-pulsar magnetosphere is actually blown away by the A-pulsar wind it is amazing that the B pulsar can pulse at all! It has also been possible to observe an eclipse of the A-pulsar signal as it passes behind the B pulsar. It turns out that the binary system is seen almost edge-on, another very fortuitous circumstance. The most direct evidence for this is the detection of the so-called Shapiro delay in the A-pulsar signal resulting from deflection of the ray path as it passes near the companion. This has an amplitude of about 100 microseconds, implying that the orbit plane is within three degrees of being edge-on. The A eclipse is very short, lasting about 30 seconds, a duration roughly consistent with occultation by the remaining part of the B-pulsar magnetosphere. Detection of the second neutron star as a pulsar opens up a whole new set of investigations in relativistic gravity. The ratio of the orbital Doppler shifts immediately gives the mass ratio of the two stars. Importantly, this ratio is largely independent of theories of gravity and hence it provides an important constraint on such theories. As Figure 3 shows, the mass-ratio and periastron-advance constraints are nearly orthogonal and hence accurately determine the two neutron-star masses: 1.337+/-0.004 solar masses and 1.251+/-0.004 solar masses. The three other relativistic constraints and the mass function constraint for the two stars are all consistent with these values, confirming the accuracy of predictions made by Einstein's general theory of relativity. In the next few years, we expect to measure several more relativistic effects, some dependent on higher-order terms in the post-Newtonian expansion. These will provide the tightest constraints yet on theories of gravity in the strong-field regime.
References: Burgay, M., D Amico, N., Possenti, A., Manchester, R.N., Lyne, A.G., Joshi, B.C., McLaughlin, M.A., Kramer, M., Sarkissian, J. M. Camilo, F., Kalogera, V., Kim, C, & Lorimer, D.R., 2003, Nature, 426, 531-533. Lyne, A.G., Burgay, M., Kramer, M., Possenti, A, Manchester, R.N., Camilo, F., McLaughlin, M.A., Lorimer, D.R., D'Amico, N., Joshi, B.C., Reynolds, J.E. & Freire, P.C.C., 2004, Science, 303, 1153-1157. |
|